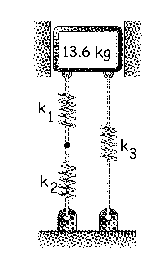
Un bloque de 13.6 kg está soportado por el -

a) k_eq=4112.5 N/m
b) T=0.361 s, ν=2.768 s^-1
c) v_máx=0.765 m/s; a_máx=13.309 m/s²
d) y=0.044e^-1.471tcos17.33t
e) v=0.174 m/s, a=-0.669 m/s²

a) Las constantes de los resortes, en el sistema internacional, son:

k₁=3.5 kN/m=3500 N/m; k₂=2.1 kN/m=2100 N/m; k₃=2.8 kN/m=2800 N/m

Los resortes k₁ y k₂ están en serie, luego podemos determinar una constante equivalente que llamaremos k_i y que será:

Tendremos ahora dos resortes en paralelo, el resorte de constante k_i y el resorte de constante k₃. Por estar en paralelo se cumplirá que la constante equivalente será:

k_eq=k_i+k₃=1312.5+2800=4112.5 N/m

k_eq=4112.5 N/m

b) Podemos considerar el sistema como un único resorte de constante k_eq. En ese caso, para una masa unida a un resorte la única fuerza es la de recuperación elástica luego tendremos:

La ecuación general de un movimiento armónico simple es:

Por tanto por comparación entre las dos ecuaciones:

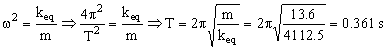
T=0.361 s

La frecuencia es el inverso del período luego:

ν=2.768 s^-1

c) Como el movimiento es armónico simple, la ecuación que nos da la posición en función del tiempo será del tipo:

y=Asen(ωt+φ₀)

donde A es la amplitud (elongación máxima ⇒ A=44 mm=0.044 m), ω es la pulsación y φ₀ es el desfase inicial (ángulo en el origen de tiempos). La velocidad por tanto será la derivada de la posición respecto del tiempo:

En esta expresión la amplitud y la pulsación son constantes, y el único término variable es el coseno. La velocidad por tanto será máxima cuando el coseno adquiera su valor máximo, que es la unidad:

v=v_máx ⇒ cos(ωt+φ₀)=1 ⇒ v_máx=Aω=A · 2πν=0.044 · 2 · π · 2.768=0.765 m/s

v_máx=0.765 m/s

Y la aceleración es la derivada de la velocidad respecto del tiempo, luego:

Igual que antes, como la amplitud y la pulsación son constantes, la aceleración será máxima cuando el seno, que es el único término variable, sera también máximo. El valor más alto que puede tomar el seno es la unidad luego:

a=a_máx ⇒ sen(ωt+φ₀)=1 ⇒ a_máx=-Aω²=A · 4π²ν²=-0.044 · 4 · π ² · 2.768²=-13.309 m/s²

En módulo:

a_máx=13.309 m/s²

d) Determinaremos antes de seguir el desfase inicial. Tenemos que en t=0 el desplazamiento coincide con la amplitud luego:

t=0 ⇒ y=A ⇒ y=Asen(ωt+φ₀) ⇒ A=Asenφ₀ ⇒ senφ₀=1 ⇒

La ecuación del movimiento es:

Nos dicen ahora que existe una fuerza de rozamiento proporcional a la velocidad y cuya constante de proporcionalidad vale 40 Ns/m. En primer lugar habrá que determinar de qué tipo de amortiguamiento se trata, calculando el parámetro de amortiguamiento. Dicho parámetro vale: