a) Pasan con la misma velocidad
b) Vuelven a la vez
c) Más fácil parar a Laura

a) Las dos pasarán por la posición vertical con la misma velocidad. Puesto que no existen rozamientos ni resistencia del aire, se debe conservar la energía mecánica total. Por tanto, toda la energía potencial que tiene cualquiera de las niñas cuando se sueltan desde el reposo debe transformarse en energía cinética al pasar por la posición más baja. Entonces tendremos:

Podemos ver que la velocidad de las niñas al pasar por la vertical no depende de la masa de las niñas, sino únicamente de la altura desde la cual son soltadas. Como ambas se dejan en libertad desde el mismo punto las dos llegarán a la posición más baja con la misma velocidad.

PASAN CON LA MISMA VELOCIDAD

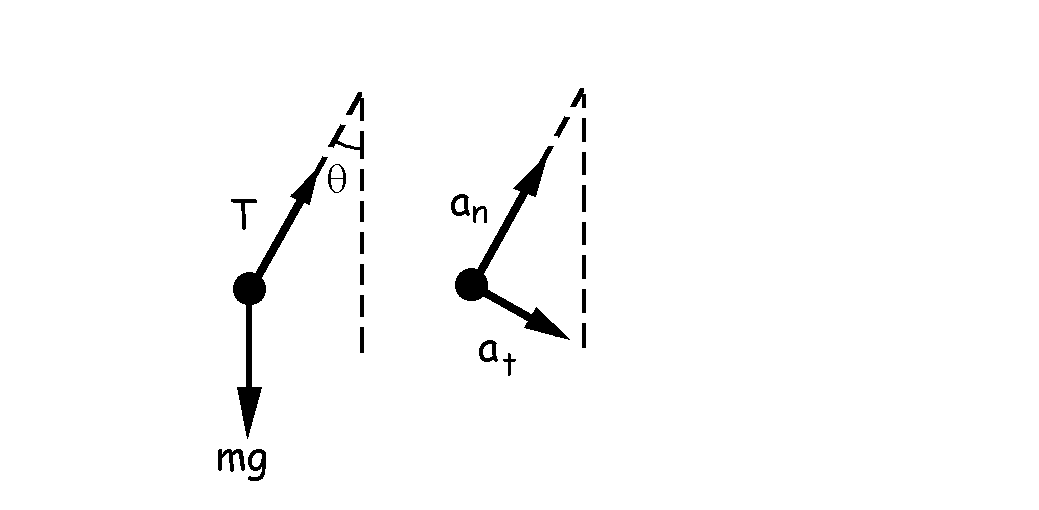b) Aislamos una cualquiera de las niñas en una posición genérica. Las fuerzas a que está sometida son la tensión de la cuerda y su peso, y dado que la trayectoria es circular las aceleraciones que tendrá serán la tangencial y la centrípeta. La aceleración centrípeta vale:

La velocidad de las niñas es igual en todo momento (ya que se debe conservar la energía total) y el radio de curvatura de la trayectoria es la longitud del columpio, lo que también será igual en los dos casos ya que los columpios son iguales. Por tanto podemos concluir que la aceleración centrípeta es igual para las dos niñas. En cuanto a la aceleración tangencial podemos aplicar la segunda ley de Newton al eje tangencial y tendremos:

ΣF_t=ma_t ⇒ mgsenθ=ma_t ⇒ a_t=gsenθ

Podemos ver por tanto que la aceleración tangencial también es igual para las dos niñas ya que no depende de su masa. Entonces, si las dos son soltadas desde el reposo y desde la misma altura y están sometidas a la misma aceleración recorrerán espacios iguales en tiempos iguales y volverán a la vez a la posición de partida.

VUELVEN A LA VEZ

Otra forma más sencilla de resolver este apartado es considerar el movimiento de las niñas como el de un péndulo simple, ya que no tenemos en cuenta rozamientos ni la resistencia del aire. Entonces el tiempo que tardan las niñas en volver de nuevo a la posición de partida será un período. Para un péndulo simple el período vale:

Como tanto l como g son iguales para ambas niñas, el período es igual en el movimiento de ambas y las dos vuelven a la vez a la posición de partida.

c) Para parar a las niñas se debe vencer a la componente tangencial de su peso, es decir, se debe ejercer una fuerza F que será:

F=mgsenθ

Dicha fuerza será tanto mayor cuando mayor sea la masa de la niña, luego será más fácil parar a la más ligera, es decir, a Laura.

MÁS FÁCIL PARAR A LAURA