a=1.307 m/s²

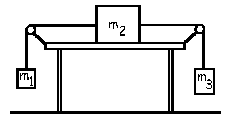
Al soltar la masa m₂ el sistema comenzará a moverse, teniendo todos los cuerpos la misma aceleración a, ya que están unidos mediante cuerdas inextensibles. Aislamos en primer lugar la masa m₁ y tendremos lo que aparece en la figura. Tomaremos como eje X el horizontal, positivo hacia la derecha, y como eje Y el vertical, positivo hacia arriba. Aplicando la segunda ley de Newton a este cuerpo:

ΣF_y=m₁a_y ⇒ T₁-m₁g=m₁a ⇒ T₁=m₁g+m₁a

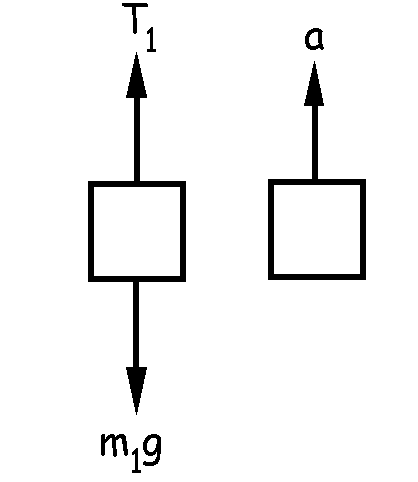
Ahora aislamos la masa m₂ y hacemos exactamente lo mismo. A través de la segunda ley de Newton llegamos a:

ΣF_x=m₂a_x ⇒ T₂-T₁=m₂a

Sustituimos el valor de T₁ por su expresión, obtenida a partir del diagrama de fuerzas de m₁:

T₂-T₁=m₂a ⇒ T₂-m₁g-m₁a=m₂a ⇒ T₂=m₁g+m₁a+m₂a

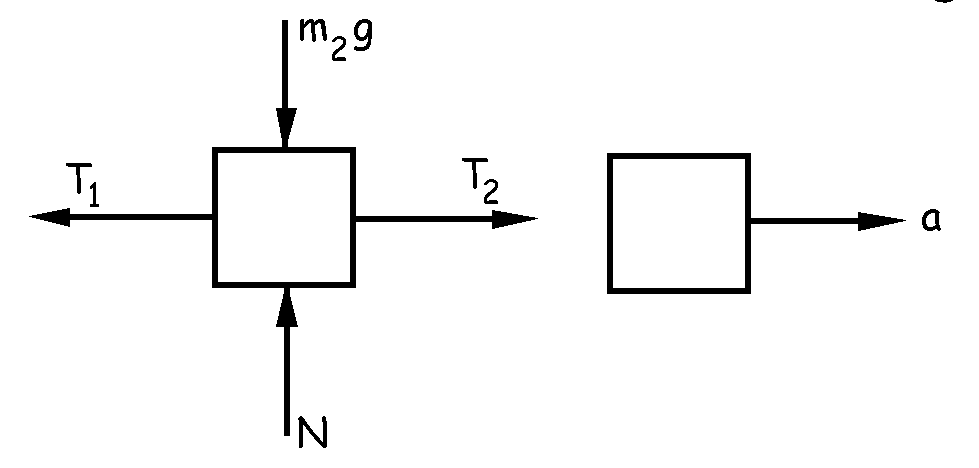
Por último hacemos el diagrama de fuerzas de m₃ y aplicamos también a este cuerpo la segunda ley de Newton:

ΣF_y=m₃a_y ⇒ m₃g-T₂=m₃a

Y sustituimos T₂ por la expresión obtenida anteriormente:

m₃g-T₂=m₃a ⇒ m₃g-m₁g-m₁a-m₂a=m₃a

m₃g-m₁g=m₁a+m₂a+m₃a ⇒ g(m₃-m₁)=(m₁+m₂+m₃)a

a=1.307 m/s²