Δy=0.4 m

En el caso de ondas que inciden perpendicularmente sobre una rendija larga y estrecha sólo la parte del frente de onda que pasa por la ranura contribuye a las ondas transmitidas o difractadas. Al observar las ondas difractadas a ángulos θ diferentes con respecto a la dirección de incidencia, encontramos que para ciertas direcciones su intensidad es cero. Estas direcciones están dadas por la relación:

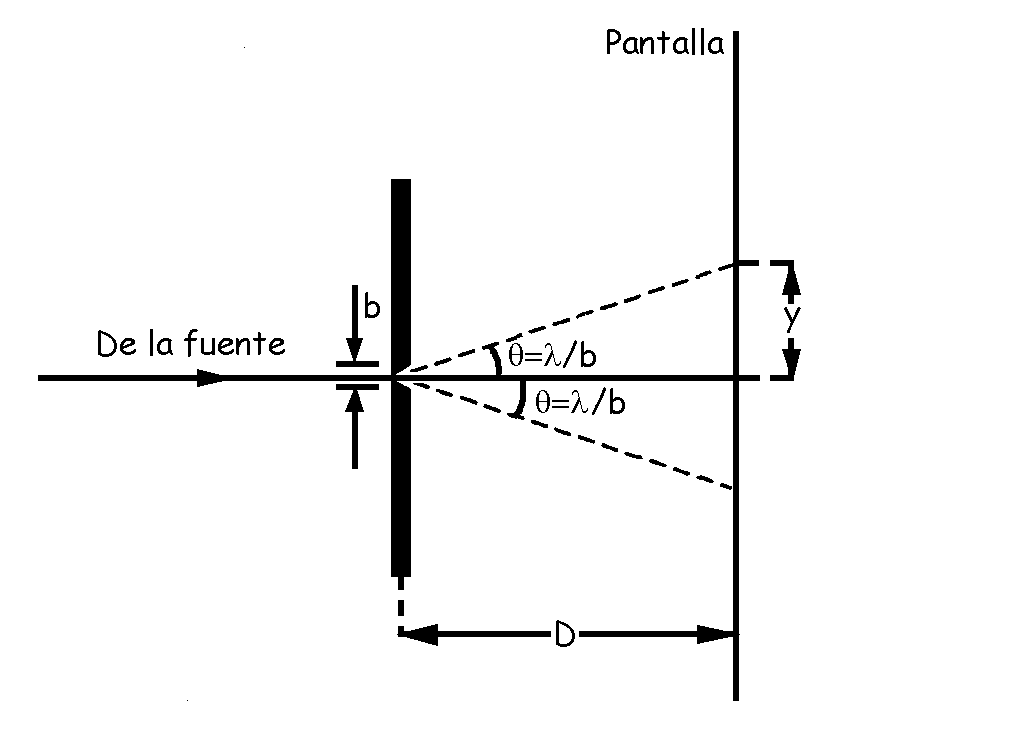donde n puede ser un número entero positivo o negativo, b es el ancho de la ranura y λ la longitud de onda. El valor de n=0 está excluido pues corresponde a una observación a lo largo de la dirección de incidencia que, obviamente, implica un máximo de iluminación. Podemos ver en la figura que si la distancia entre la pantalla y la rendija (D) es mucho mayor que el ancho de la rendija (b), el ángulo θ es muy pequeño y el seno puede aproximarse a la tangente, con lo que tendremos que los mínimos se producen en:

de donde podemos obtener la separación espacial entre los mínimos. Para el mínimo siguiente (orden n+1) tendremos pues:

Por tanto la separación espacial entre dos mínimos consecutivos es:

La separación espacial es la misma para cualquier mínimo consecutivo, y vale:

Δy=0.4 m