Para que el sistema pueda reducirse a un vector único el invariante escalar debe ser nulo:

F·M=0 Þ
(-i+2j+3k)·(4i+2j)=-4+4=0

Como dicho invariante es nulo el sistema puede reducirse a un vector. En la figura puede verse cómo se transforma el vector y el par a un único vector de valor F aplicado en un punto (x, y, 0) del plano XY. El valor del vector obviamente será F:

F=-i+2j+3k

 

Para que el momento sea nulo y el sistema quede reducido únicamente a un vector podemos ver en la figura que el momento de F respecto del punto (x, y, 0) debe valer –M, ya que así los momentos se anularían. Entonces:

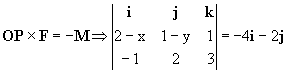
3(1-y)i+j+2(2-x)k+(1-y)k-2i-3(2-x)j=-4i+2j

 

Igualando componentes en el eje X:

 

E igualando componentes en el eje X:

 

Podemos comprobar con la última ecuación, es decir, igualando componentes en el eje Z: