a) ε=0.107
b) a=7330 km
c) T=1.73 h
d) v_A=23892 km/h; h_A=1744 km

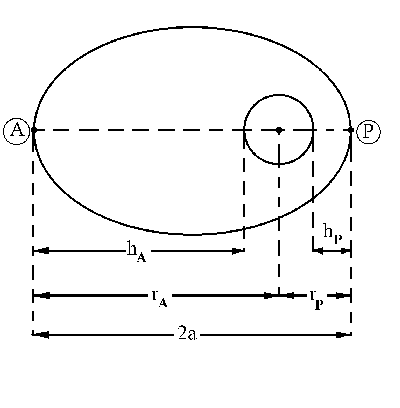a) Tendremos la trayectoria que aparece en la figura. Llamaremos M a la masa de la Tierra, R a su radio y m a la masa del satélite. Los datos que conocemos son:

r_P=h_P+R=175+6370=6545 km; v_P=29620 km/h=8227.8 m/s

La ecuación de la cónica es:

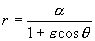
La ascensión recta la podemos determinar a través del momento angular:

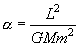
Como el momento angular es constante, lo podemos determinar en cualquier punto. Hay dos puntos que son especialmente sencillos, que son el apogeo y el perigeo (A y P). En ellos la velocidad es perpendicular al vector de posición, por lo que el momento angular es el producto del vector de posición por la cantidad de movimiento (como el ángulo que forman ambos vectores es de 90^º, el seno vale la unidad). Si aplicamos esto al perigeo tendremos:

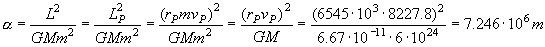
Luego la ecuación de la cónica nos queda:

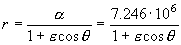
Conocemos un punto de la cónica, que es el perigeo. Cuando r=r_P ⇒ θ=0^o ⇒ cosθ=1 con lo cual tenemos la expresión:

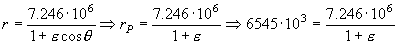
De donde obtenemos:

ε=0.107

 

b) Ahora tenemos una ecuación de la cónica que es:

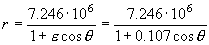
Cuando r=r_A ⇒ θ=180^o ⇒ cosθ=-1 y nos queda la expresión:

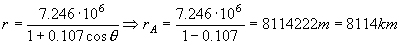
Por tanto el semieje mayor es:

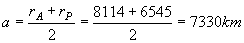
a=7330 km

 

c) El período lo podemos obtener por aplicación de la tercera ley de Kepler, según la cual los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores. Entonces:

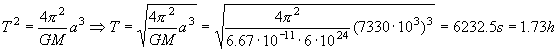
T=1.73 h

 

d) Aplicamos la conservación del momento angular entre los puntos A y P:

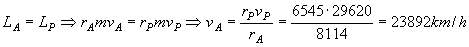
v_A=23892 km/h

Y la altura en este punto:

h_A=r_A-R=8114-6370=1744 km

h_A=1744 km