hmáx=15164 km; hmín=1452 km
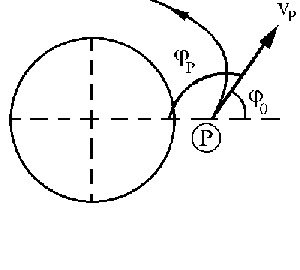
Llamaremos P al punto de lanzamiento, M a la masa de la Tierra, R a su radio y m a la masa del satélite. El ángulo φ P que forma el radio vector con la velocidad es:
φo=75º
Y la velocidad en el punto P también es conocida:
vP=8000 m/s
Si A es el punto de altura máxima, en él el radio vector es perpendicular a la velocidad. Por ello, el momento angular será el producto del radio vector por la cantidad de movimiento (como el ángulo que forman estos dos vectores es de 90º, el seno será la unidad). Por conservación del momento cinético tendremos:
LA=LP ⇒ rAmvA=rPmvPsenφP ⇒ rAvA=rPvPsenφP
El radio en el punto P es:
rP=hP+R=2400+6370=8770 km
Tendremos entonces:
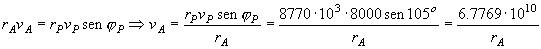
Siendo φp=180º-75º=105º
Además, se conserva la energía total, por lo que si aplicamos esto a los puntos A y P:
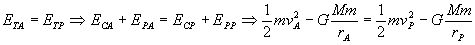
Sustituímos los valores conocidos y la expresión que hemos obtenido para vA:
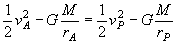
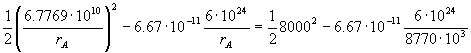
Tenemos una ecuación con una incógnita, rA. La ecuación es de segundo grado, lo que hace que aparezcan dos soluciónes, que son:
rA1=21533923 m=21534 km; rA2=7822076 m=7822 km
Como A es el punto de altura máxima, obviamente tendremos que el radio máximo será el más grande, es decir:
rmáx=rA1=21534 km
Y la altura máxima:
hmáx=rmáx-R=21534-6370=15164 km
hmáx=15164 km
Consideremos ahora el punto B de altura mínima. En él ocurre exactamente lo mismo que antes, el radio vector es perpendicular a la velocidad, por lo que en la expresión del momento angular no aparecería el seno del ángulo que forman (sería la unidad). Planteando las ecuaciones de conservación del momento angular y de la energía total entre los puntos B y P puede verse que tendríamos exactamente las mismas ecuaciones que cuando las hemos planteado para los puntos A y P. Llegaríamos entonces a las mismas dos soluciones que serán ahora:
rB1=21533923 m=21534 km; rB2=7822076 m=7822 km
El punto B le hemos definido como el de altura mínima, luego la solución válida será la más pequeña:
rmín=rB2=7822 km
Y la altura:
hmín=rmín-R=7822-6370=1452 km
hmín=1452 km