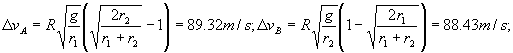
Llamaremos M a la masa de la Tierra, R a su radio y m a la masa del vehículo espacial. El valor de la gravedad en la superficie terrestre es:
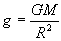
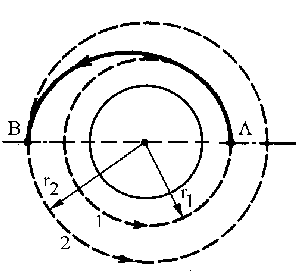
Vamos a determinar en primer lugar el incremento ΔvA. Inmediatamente antes del incremento de velocidad, el vehículo está en el punto A en la órbita circular de radio r1, y su velocidad es vA. Por ser una órbita circular la única fuerza que actúa sobre el vehículo es la de atracción gravitatoria, y la única aceleración es la normal o centrípeta, ya que el movimiento en esta órbita es circular y uniforme. Como tanto la fuerza como la aceleración tienen la misma dirección y sentido tendremos por aplicación de la segunda ley de Newton:
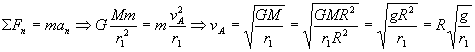
Inmediatamente después del incremento de velocidad, la velocidad del vehículo será v´A, estará en el mimso punto A pero ya en la trayectoria elíptica. Para la trayectoria elíptica se conserva la energía luego:
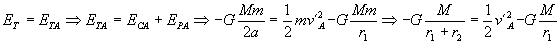
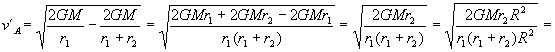
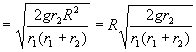
La variación de velocidad en el punto A será la diferencia entre las velocidades después y antes del incremento:
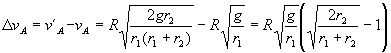
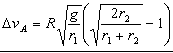
Ahora pasamos al punto B y procedemos de modo análogo. Inmediatamente antes del incremento de velocidad, el vehículo estará en el punto B, su velocidad es vB y se encuentra en la órbita elíptica. En la órbita elíptica se conserva el momento angular. Los puntos A y B tienen además la ventaja de que el radio vector es perpendicular a la velocidad, por lo que el momento angular es el producto del radio vector por la cantidad de movimiento (el ángulo que forman estos vectores es de 90º por lo que el seno vale la unidad). Aplicando la conservación del momento angular entre estos dos puntos:
LA=LB ⇒ r1mv´A=r2mvB
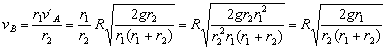
Inmediatamente después del incremento de velocidad, el vehículo está en ese mismo punto B, pero la velocidad es v´B y se encuentra en la órbita circular. Por ser la órbita circular la única fuerza que hay es la de atracción gravitatoria y la única aceleración es la normal o centrípeta. A través de la segunda ley de Newton tendremos:
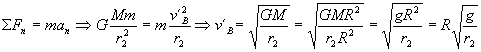
El incremento de velocidad es la diferencia entre las velocidades después y antes del incremento:
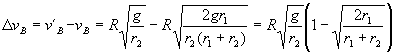
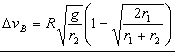
Si sustituímos los datos numéricos tendremos:
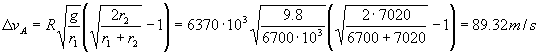
ΔvA=89.32 m/s
Y en el punto B tendremos:
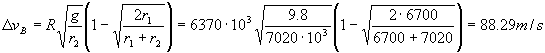
ΔvB=88.29 m/s
La razón por la que siendo los dos incrementos de velocidad positivos la velocidad en la órbita 2 es menor que en la 1, es porque estos dos incrementos no se producen uno después del otro. En el punto A antes del incremento de velocidad el vehículo tiene una velocidad que hemos determinado como:
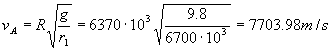
Sobre esta velocidad se produce el primer incremento de velocidad ΔvA de modo que nos queda una nueva velocidad v´A:
v´A=vA+ΔvA=7703.98+89.32 =7793.30 m/s
El vehículo está en este instante en la órbita elíptica y en el punto A. El segundo incremento de velocidad no se produce en el punto A, sino en el punto B. Desde A hasta B en la órbita elíptica aumenta el radio, luego disminuye la velocidad, de modo que en B el vehículo llega con una velocidad:
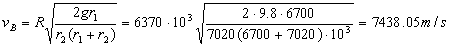
De modo que desde A hasta B se ha producido un incremento de velocidad negativo con el que antes no habíamos contado, y que vale:
ΔvAB=vB-v´A=7438.06-7793.30=-355.24 m/s
Por último, en el punto B se produce el último incremento de velocidad, que es positivo, ΔvB. De manera que en total, el incremento completo de velocidad es:
Δv=ΔvA+ΔvB+ΔvAB=89.32+88.29-355.24=-177.63 m/s
Es decir, que el incremento real de velocidad es negativo, por lo que la velocidad en la órbita 2 es menor que en la 1.