Problema de Gravitación

El programa de un vuelo no tripulado para explorar el planeta Marte establece que el vehículo de regreso a la Tierra describirá en primer lugar una órbita circular alrededor del planeta. Al pasar por el punto A será transferido a una órbita elíptica de transición encendiendo sus motores para aumentar su velocidad en ΔvA. Cuando pase por el punto B, el vehículo volverá a ser transferido a una segunda órbita de transición, disminuyendo la velocidad en ΔvB. Finalmente, al pasar el vehículo por el punto C se aumentará su velocidad en ΔvC para situarlo en la trayectoria parabólica de retorno. Sabiendo que el radio del planeta Marte es R=3400 km, que su masa es 0.108 veces la masa de la Tierra y que las alturas de los puntos A, B y C son dA=2500 km, dB=90000 km y dC=1000 km respectivamente, determinar: a) el aumento de velocidad ΔvA que es necesario proporcionar al vehículo en el punto A para transferirlo a la primera órbita de transición; b) la variación de velocidad ΔvB que es necesario proporcionar al vehículo en el punto B para transferirlo a la segunda órbita de transición; c) el aumento mínimo de velocidad ΔvC que es preciso proporcionar al vehículo en el punto C para situarlo en una trayectoria de escape; d) el tiempo empleado por el vehículo para recorrer la primera órbita de transición entre los puntos A y B.

a) ΔvA=1005.66 m/s
b) ΔvB=-30.44 m/s
c) ΔvC=100.76 m/s
d) t=46 h 26 min 18 s

a) La masa de Marte, a la que denominaremos con la letra M, será:

M=0.108MT=0.108 · 6 · 1024=6.48 · 1023 kg

Los radios en los puntos A, B y C son:

rA=dA+R=2500+3400=5900 km; rB=dB+R=90000+3400=93400 km; rC=dC+R=1000+3400=4400 km

En el punto A, inmediatamente antes del incremento de velocidad, el vehículo se encuentra en una órbita circular de radio rA con una velocidad vA. En la órbita circular la única fuerza que actúa sobre el vehículo es la de atracción gravitatoria, y por tanto la aceleración que existe es la normal o centrípeta. Fuerza y aceleración tienen la misma dirección y sentido, por lo que aplicando la segunda ley de Newton tendremos:

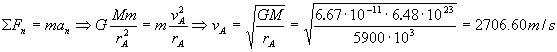
Inmediatamente después del incremento de velocidad, el vehículo se encuentra en ese mismo punto A, pero en la órbita elíptica, con una nueva velocidad v´A, y el eje mayor de la elipse es:

2a1=rA+rB=5900+93400=99300 km

En esta órbita se mantiene constante la energía, luego tendremos:

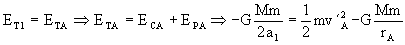
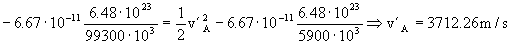
El incremento de velocidad es entonces:

ΔvA=v´A-vA=3712.26-2706.60=1005.66 m/s

ΔvA= 1005.66 m/s

 

b) En el punto B, inmediatamente antes del incremento de velocidad, el vehículo se encuentra en la primera órbita de transición con velocidad vB. En esta órbita se conserva el momento angular. Además, en los puntos A y B el radio vector es perpendicular a la velocidad, por lo que el momento angular es el producto del radio vector por la cantidad de movimiento (como ambos vectores forman un ángulo de 90º, el seno es la unidad). Por conservación del momento angular tenemos:

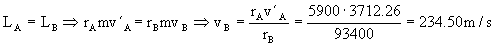
En el punto B, inmediatamente después del incremento de velocidad, el vehículo se encuentra en la segunda órbita de transición, su velocidad es v´B y el eje mayor de esta órbita es:

2a2=rB+rC=93400+4400=97800 km

En esta órbita se conserva la energía total, luego tendremos:

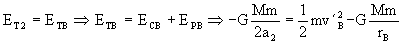
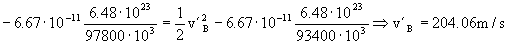
La variación de velocidad en el punto B es por tanto:

ΔvB=v´B-vB=204.06-234.50=-30.44 m/s

ΔvB= -30.44 m/s

 

c) En el punto C justo antes del incremento de velocidad, el vehículo está en la segunda órbita elíptica de transición, con una velocidad vC. En esta órbita se conserva el momento angular, y en los puntos B y C ocurre, como ya hemos explicado antes, que el radio vector es perpendicular a la velocidad, por lo que se simplifica el cálculo del momento angular. Por conservación de este parámetro tenemos:

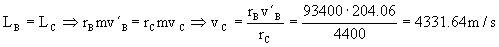
En el punto C, inmediatamente después del incremento de velocidad , el vehículo se encuentra en una trayectoria parabólica con velocidad v´C. En una trayectoria parabólica la energía total es nula luego:

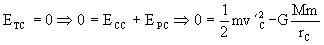
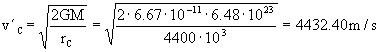
El incremento de velocidad en el punto C es:

ΔvC=v´C-vC=4432.40-4331.64=100.76 m/s

ΔvC= 100.76 m/s

 

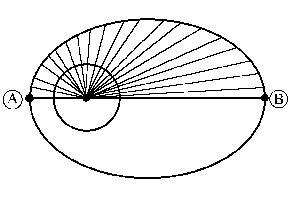d) En una órbita elíptica, como es la primera órbita de transición, la velocidad areolar es constante, es decir, el tiempo invertido en recorrer un cierto tramo es proporcional al área barrida por el radio vector, siendo el período T el tiempo empleado en barrer el área completa de la elipse S. Como puede verse en el gráfico, donde sólo aparecería la órbita que nos interesa, cuando el vehículo se traslada desde el punto A al punto B el radio vector barre media elipse. Teniendo en cuenta lo que acabamos de explicar, y llamando t al tiempo que tarda el vehículo en ir desde A hasta B tendremos:

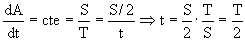
Y el período lo podemos determinar aplicando la tercera ley de Kepler, que dice que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores. Nos queda:

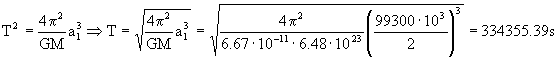
Por tanto el tiempo t vale:

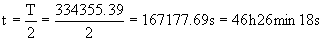
t=46 h 26 min 18 s