Problema de Gravitación

Tras completar su misión de exploración en la Luna los astronautas que componen la tripulación de un módulo de exploración lunar Apolo se disponen a reunirse con el módulo de mando que está en órbita sobre la Luna a 140 km de altura. Para ello encienden los motores del módulo lunar y siguen una trayectoria curva hasta un punto A, 8 km por encima de la superficie lunar, donde apagan los motores. Sabiendo que en ese instante el módulo lunar se mueve paralelamente a la superficie de la Luna y que seguirá avanzando a lo largo de una trayectoria elíptica para encontrarse con el módulo de mando en el punto B, determinar: a) la velocidad del módulo lunar al apagarse los motores; b) la velocidad relativa con que el módulo de mando alcanzará al módulo lunar; c) una vez que el módulo lunar se incorpora al módulo de mando, la nave espacial Apolo gira sobre sí misma para que el módulo lunar quede mirando hacia atrás. Después de recorrer una órbita completa, cuando la nave vuelve a pasar por el punto B, el módulo lunar es lanzado a la deriva y se estrella contra la superficie lunar en el punto C. Determinar su velocidad relativa respecto al módulo de mando cuando es lanzado a la deriva, sabiendo que el ángulo BOC es de 90o. El punto B es el apogeo de la trayectoria elíptica de choque.

a) vA=1687.4 m/s
b) vrel=29.34 m/s
c) vrel=-63.07 m/s

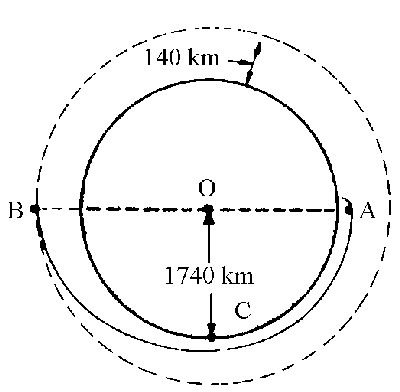
a) Llamaremos M a la masa de la Luna, R a su radio, mM a la masa del módulo de mando y mL a la masa del módulo lunar. Los radios conocidos en los puntos A y B son:

rA=hA+R=8+1740=1748 km

rB=hB+R=140+1740=1880 km

Y el eje mayor de esta cónica:

2a=rA+rB=1748+1880=3628 km

Los motores se apagan en el punto A, e inician una trayectoria elíptica, en la cual se conserva la energía total. Determinando dicha energía en el punto A tendremos:

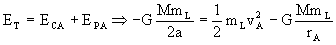
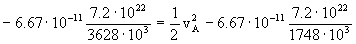
De donde obtenemos:

vA=1687.40 m/s

 

b) El módulo lunar y el módulo de mando se unen en el punto B, luego habrá que determinar las velocidades de ambos vehículos en ese punto, para así calcular la velocidad relativa por diferencia entre ambas. Para el módulo lunar, éste se encuentra en una órbita elíptica, en la cual se conserva el momento angular. Además, en los puntos A y B el radio vector es perpendicular a la velocidad, por lo que el momento angular es el producto del radio vector por la cantidad de movimiento (el ángulo que forman ambos vectores es de 90º y su seno será la unidad). Aplicando la conservación del momento angular entre los puntos A y B tendremos que la velocidad del módulo lunar en B, vB es:

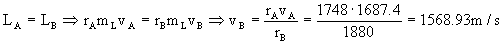
El módulo de mando se encuentra en una órbita circular de radio rB, luego en esta órbita por estár sometido únicamente a la fuerza de atracción gravitatoria, y por ser el movimiento circular tiene sólo aceleración normal o centrípeta. Como la fuerza y aceleración centrípeta tienen la misma dirección y sentido, aplicando la segunda ley de Newton:

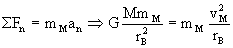
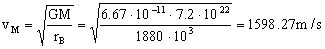
Entonces la velocidad del módulo de mando respecto del módulo lunar será la diferencia entre ambas:

vM/L=vM-vL=1598.27-1568.93=29.34 m/s

vM/L= 29.34 m/s

 

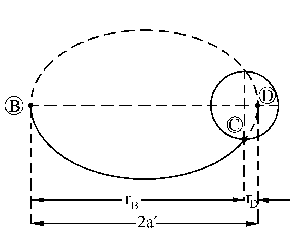c) Ahora tenemos una nueva órbita de aterrizaje, tal como la que hemos dibujado. A los parámetros de esta órbita los representaremos con primas para distinguirla de la otra órbita elíptica. Para determinar la velocidad relativa del módulo lunar respecto del módulo de mando cuando es lanzado a la deriva necesitamos las velocidades tanto del módulo lunar como del módulo de mando en el punto B, donde se inicia la trayectoria de aterrizaje. El módulo de mando está en la trayectoria circular, luego su velocidad es constante y vale:

vM=1598.27 m/s

El módulo lunar se encuentra en la órbita de aterrizaje. Para calcular su velocidad en el punto B necesitamos conocer la energía total en la órbita, por lo que nos hace falta el parámetro 2a´. Para determinarlo vamos a utilizar la ecuación de la cónica. Esta ecuación es:

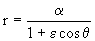
Conocemos dos puntos de la cónica. Para el punto C de aterrizaje:

r=R y θ=-90º ⇒ cosθ=0

Con lo que nos queda la expresión, sustituyendo en la ecuación de la cónica:

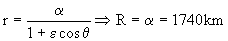
Entonces la ecuación de la cónica nos queda:

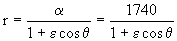
Conocemos además el punto B, para el cual:

r=rB y θ=180o ⇒ cosθ=-1

Con lo que tendremos:

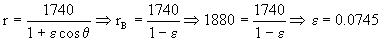
Tenemos ya la ecuación de la trayectoria:

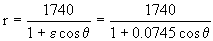
En esta ecuación, para el punto D tendremos:

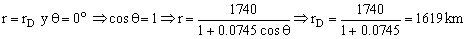
Con los radios de los puntos B y D podemos obtener el eje mayor:

2a´=rB+rD=1880+1619=3490 km

En la órbita de aterrizaje se conserva la energía total, luego si la determinamos en el punto B, donde se deja al módulo lunar a la deriva:

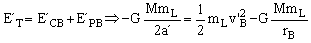
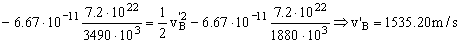
Por tanto la velocidad relativa del módulo lunar respecto del módulo de mando en el punto B es:

V’B/M=v’B-vM=1535.20-1598.27=-63.07 m/s

Vrel=V’B/M=-63.07 m/s