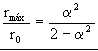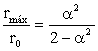
Llamaremos M a la masa del cuerpo celeste indeterminado, y m a la de la nave espacial. Inicialmente la nave está en una órbita circular de radio r0. En dicha órbita la única fuerza que actúa sobre la nave es la de atracción gravitatoria, y la única aceleración que tiene, dado que el movimiento es uniforme, es la normal o centrípeta. Como fuerza y aceleración tienen la misma dirección y sentido, aplicando la segunda ley de Newton:
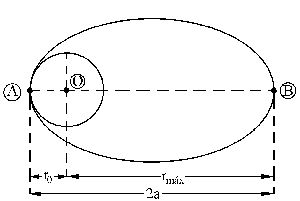Al pasar por un cierto punto, que llamaremos punto A, la nave aumenta su velocidad hasta αv0 y empieza a recorrer una órbita elíptica, siendo este punto el de mayor cercanía al cuerpo celeste de centro O. Al punto más lejano de O lo llamaremos punto B, y tendremos entonces la trayectoria que aparece en el gráfico.
En la trayectoria elíptica se conservan tanto el momento angular como la energía total. Aplicaremos la conservación de estas dos magnitudes a los puntos A y B: estos puntos presentan además la ventaja de que en ellos el radio vector es perpendicular a la velocidad, por lo que el momento angular es el producto del radio vector por la cantidad de movimiento (el ángulo que forman ambos vectores es de 90º y su seno será la unidad). Tendremos entonces las ecuaciones:
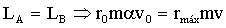
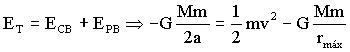
donde hemos llamado v a la velocidad de la nave en el punto B de la trayectoria elíptica. Elevamos la primera ecuación al cuadrado, y en la segunda sustituiremos el parámetro 2a por su valor que puede verse en el gráfico:
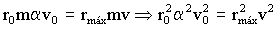
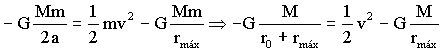
De la primera ecuación podemos despejar v2 y tendremos:
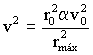
Sustituímos el valor que hemos obtenido de v0 al inicio del problema:
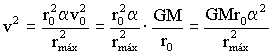
De la ecuación de la energía, si despejamos también v2 obtenemos:
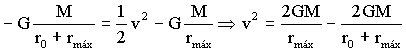
Igualando las dos expresiones de v2:
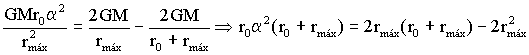
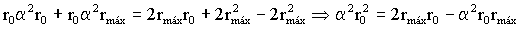
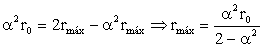
Como podemos ver en esta última expresión, la distancia máxima rmáx depende únicamente de α y de r0, como queríamos demostrar.
Si dividimos los dos miembros por r0 obtenemos el cociente que buscamos:
