G=-2πGσk para z>0
G=2πGσk para z<0
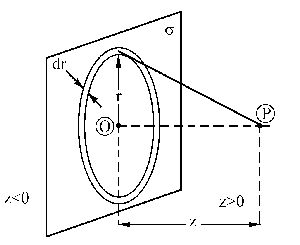
Dividiremos el plano en anillos concéntricos de radio r y espesor dr centrados en el eje Z, tal como se muestra en la figura. El potencial en puntos del eje Z valdrá:
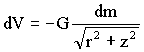
donde dm es la masa del anillo elegido. Esta masa valdrá:
dm=σdS=σ2πrdr
siendo dS el área del anillo. Sustituyendo esto en la expresión del potencial:
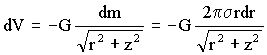
Integramos en primer lugar para puntos situados a la derecha del plano, es decir, para z>0, con lo que los límites de la integral variarán entre cero e infinito:
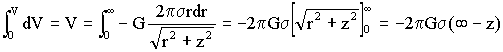
Nos interesa realmente la diferencia de potencial entre el plano y un punto exterior a él. Tomaremos entonces un origen arbitrario de potencial, por ejemplo, supondremos que el potencial es nulo cuando z=∞, con lo cual eliminaríamos el primer término de la ecuación y nos quedaría:
V=2πGσz
Con lo cual el campo:
g=-gradV=-2πGσ
Si nos fijamos en el gráfico, el campo tiene la dirección de la recta que une el punto P con el anillo. Para cualquier punto del anillo que tomemos, siempre existe su simétrico en la parte de abajo del anillo, de modo que las componentes verticales del campo serían iguales y de signo contrario, con lo que se anularían, y sólo nos quedan las componentes en la dirección del eje Z, que se suman. Por tanto vectorialmente el campo tiene la dirección del eje Z:
g=-2πGσk para z>0
Para puntos al otro lado del anillo (z<0) únicamente cambian los límites de la integral, que irán desde infinito hasta cero, con lo cual obtenemos la misma solución pero con el signo cambiado:
V=-2πGσz
Y el campo:
g=-gradV=2πGσ
Vectorialmente, como tiene la dirección del eje Z:
g=2πGσk para z<0