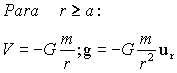
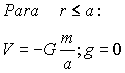
Si llamamos σ a la densidad superficial de la esfera tendremos:
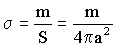
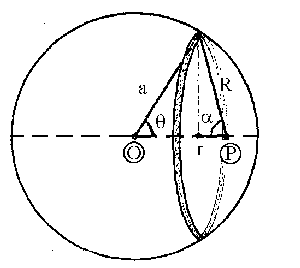
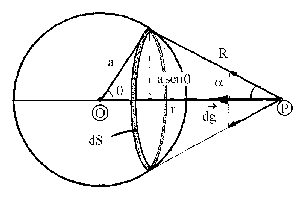Tomamos como elemento diferencial una cinta alrededor de la esfera, tal como se muestra en la figura, cuyo espesor será adθ y cuyo radio será asenθ. Tomaremos en primer lugar puntos exteriores a la esfera, tales como el punto P que aparece en la figura. El potencial valdrá:
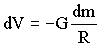
La superficie del elemento diferencia es:
dS=2πasenθadθ=2πa2senθdθ
Y la masa:
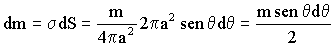
Por tanto el potencial:
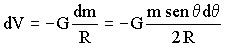
Tenemos dos variables, θ y R, que tendremos que relacionar. Por el teorema del coseno:
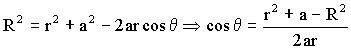
Diferenciando esa expresión:
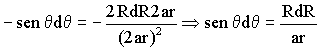
Entonces el potencial:
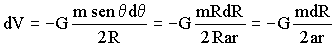
Ahora integramos entre los límites de R, que serán r-a y r+a:
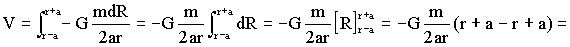
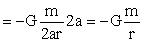
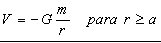
Para puntos interiores a la corteza (r≤a) llegaríamos a la misma expresión de dV, pero cambiarían los límites de la integral, que irían ahora desde a-r hasta a+r, como puede observarse en la figura. Obtendríamos:
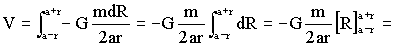
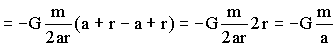
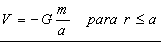
Para determinar el campo gravitatorio en un punto exterior a la corteza, observaremos en primer lugar en la primera figura que cada elemento de superficie produce en P un campo gravitatorio que tien dos componentes, una componente transversal (dirigida perpendicularmente al eje OP) y una componente radial dirigida hacia el centro de la esfera. Las componentes transversales dan una resultante nula el extender la suma (o integral) a todos los elementos de la corteza esférica. Las componentes radiales dan una resultante no nula, dirigida hacia el centro de la esfera. Podemos determinar el campo teniendo en cuenta que es el gradiente del potencial cambiado de signo:
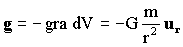
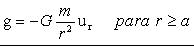
Para puntos interiores a la capa el potencial era constante, luego su derivada será nula:
g=-gradV=0
g=0 para r≤a