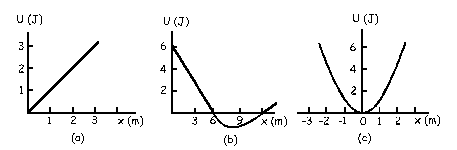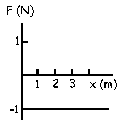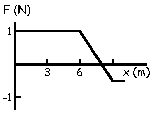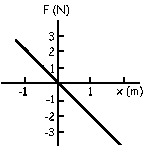
; ;

a) Para todos los casos tendremos que la fuerza es el gradiente del potencial cambiado de signo, es decir:

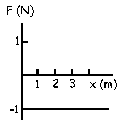En este primer caso tenemos que el potencial sigue una ecuación del tipo:

U=x

ya que es una recta que pasa por el origen y que tiene una pendiente de 45º. Entonces la fuerza será:

Luego la fuerza es constante y vale -1 N. En la gráfica podemos ver la representación.

b) Entre los puntos x=0 y x=6 tenemos que el potencial sigue la ecuación de una recta de pendiente negativa y cuya ordenada en el origen vale 6. Entonces será una ecuación del tipo:

U=b-ax=6-ax

Y conocemos también el punto en que:

x=6 ⇒ U=0

Aplicando a este punto la ecuación del potencial:

U=6-ax ⇒ 0=6-6a ⇒ a=1

Por tanto en este tramo la ecuación del potencial es:

U=6-ax=6-x

Y la fuerza en este intervalo será:

En este intervalo la fuerza es constante y vale 1 N.

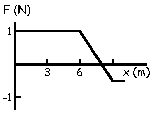Entre los puntos x=6 y x=12 la ecuación del potencial es de segundo grado. Los datos no son suficientes para determinar la ecuación. En cualquiera de los casos, tendríamos una ecuación de segundo grado, cuya derivada será una ecuación de primer grado, es decir, una recta. Entre x=6 y el vértice de la curva (algo antes de x=9) tendremos que la pendiente de la tangente es negativa, luego los valores de la fuerza serán positivos. En el vértice de la curva, la fuerza tomará un valor cero, ya que la tangente a la curva es horizontal, luego la pendiente es cero. Después de este punto la pendiente de la tangente a la curva del potencial es positiva, luego la fuerza empieza a tomar valores negativos. Además, la pendiente es menos pronunciada, luego en valor absoluto la fuerza será menor de la unidad. El gráfico será el que aparece en la figura.

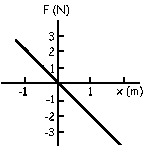c) Tenemos la ecuación de una parábola centrada, luego será del tipo:

U=x²

 

La fuerza por tanto será:

Esto es la ecuación de una recta que pasa por el origen y cuya pendiente es 2, es decir, que para todos los valores de x la y toma un valor que es justo el doble. En la figura podemos ver la representación.