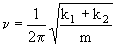a)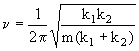 
b)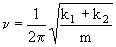 
c)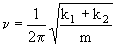 
a) Llamaremos en todo el problema eje X al eje horizontal (positivo hacia la derecha) que es donde se produce el movimiento, y eje Y al eje vertical (positivo hacia arriba). Obviamente el sistema estará en equilibrio cuando ambos resortes estén sin deformar. Supongamos que desplazamos el sistema una cantidad x hacia la derecha y lo dejamos en libertad. Cada resorte se alargará una cierta cantidad (x1 y x2 respectivamente), pero cumpliéndose que:
x1+x2=x
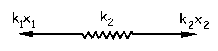Aislamos en primer lugar el resorte 2 y tenemos en cuenta que no tiene masa, luego:
ΣFX=0 ⇒ k1x1-k2x2=0 ⇒ k1x1=k2x2 ⇒ 
Entonces:
Y derivando esta ecuación dos veces respecto del tiempo:
A continuación aislamos la masa m y aplicamos la segunda ley de Newton:
Teniendo en cuenta lo que hemos obtenido en el resorte 2:
Tenemos la ecuación de un movimiento armónico simple del tipo:
Por tanto por comparación la frecuencia angular será:
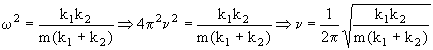
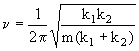
b) Como en el caso anterior, la masa estará en equilibrio cuando los resortes estén sin deformar. Supongamos ahora que desplazamos la masa m una cantidad x hacia la derecha y la dejamos oscilar. Por la geometría del sistema los dos resortes se deformarán la misma cantidad x. Tendremos entonces que por la segunda ley de Newton:
Tenemos otra vez la ecuación de un movimiento armónico simple del tipo:
Por comparación la frecuencia será:
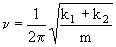
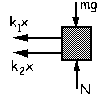
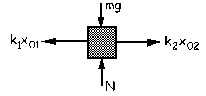c) En este tercer caso los resortes sí pueden estar deformados en el equilibrio, con la condición de que ambos estén en compresión o ambos en extensión. Supongamos que ambos están en extensión. Si trazamos el diagrama de sólido libre de la masa en la situación de equilibrio tendremos:
ΣFX=0 ⇒ k2x02-k1x01=0
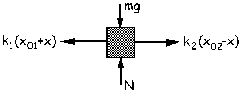Ahora desplazamos la masa m una distancia x hacia la derecha y la dejamos oscilar. El resorte 1 estará estirado ahora una cantidad x01+x mientras que el resorte 2 lo estará x02-x. Si aplicamos la segunda ley de Newton:
Si tenemos en cuenta la condición de equilibrio nos queda sólo:
Tenemos la ecuación de un movimiento armónico simple del tipo:
Por comparación la frecuencia será:
