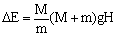a) 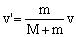
b) 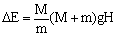
a) Tendremos que como no existen fuerzas externas la cantidad de movimiento debe conservarse entre antes y después del choque. Antes del choque tenemos la masa m moviéndose con velocidad v, y el péndulo en reposo. Después del choque todo el sistema (masa y péndulo) están unidos moviéndose con la misma velocidad v’. Se cumplirá entonces que:
![]()
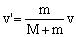
b) Ahora vamos a ver qué ocurre con las energías. Tomamos como nivel de energía potencial gravitatorio nulo la posición más baja del péndulo. Tendremos entonces que antes del choque la única energía sería la cinética de la masa m, ya que tanto la masa como el péndulo estarían a la altura del nivel cero de energía potencial gravitatoria. Después del choque, en el punto más alto de la trayectoria, la energía cinética será nula y sólo tendremos energía potencial gravitatoria correspondiente a la altura H (del péndulo y la masa, que están unidos). Entonces:
![]()
![]()
La variación de energía será por tanto:
![]()
Podemos aplicar la conservación de la energía total entre el instante posterior al choque, cuando masa y péndulo se mueven con velocidad v’ (1), y el instante en que ambos están en el punto de máxima altura (2). Entonces:
![]()
Sustituyendo la velocidad v’ por el valor que hemos obtenido en el apartado anterior:
![]()
Y sustituyendo esto en la expresión que nos da la variación de energía:
![]()
![]()