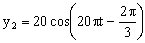Cuestion de Movimiento Ondulatorio

Dos sistemas idénticos formados por un resorte y una masa están colgados el uno al lado del otro. En el instante t=0, se suelta uno de ellos desde un punto situado 20 cm por debajo de su posición de equilibrio, vibrando con un período de 0.10 s. Cuando esta masa alcanza su posición más alta, se suelta la segunda desde un punto situado 30 cm por debajo de su posición de equilibrio. Escribir las ecuaciones de movimiento de cada una de las dos masas. ¿Y si se suelta la segunda masa cuando la primera está en y=-10 cm y va hacia arriba?

y1=20cos(20πt); y2=-20cos(20πt); y1=20cos(20πt);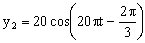

Para la primera masa tenemos que la amplitud es de 20 cm mientras que para la segunda es de 30 cm. La frecuencia angular será la misma en ambos casos puesto que los resortes son idénticos:

La ecuación de la primera masa será:

y1=A1sen(ωt+φ01)

siendo A1 la amplitud, ω la frecuencia angular y φ01 el desfase inicial (ángulo cuando t=0):

y1=A1sen(ωt+φ01)=20sen(20πt+φ01)

Podemos determinar ese desfase teniendo en cuenta que:

t=0 ⇒ y’01=-20 ⇒ -20=20senφ01 ⇒ senφ01=-1 ⇒ φ01=

Nos queda entonces la ecuación del movimiento para el primer resorte:

y1=20cos(20πt)

La segunda masa se suelta desde la posición más baja cuando la primera está en la posición más alta. Estarán por tanto desfasadas medio período, es decir, π radianes. La ecuación de esta segunda masa será:

y2=20cos(20πt-π)=-20cos(20πt)

y2=-20cos(20πt)

En el segundo caso tendremos que la ecuación de la primera masa no varía:

y1=20cos(20πt)

La segunda masa se suelta cuando la primera se encuentra en y=-10 cm. El ángulo que se ha desplazado la primera masa es:

y1=20cos(20πt) ⇒ -10=20cos(20πt) ⇒ -0.5=cos(20πt) ⇒

Luego ambos resortes están desfasados esa cantidad. La ecuación de la segunda masa será: