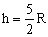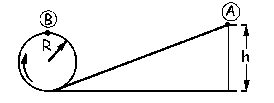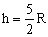
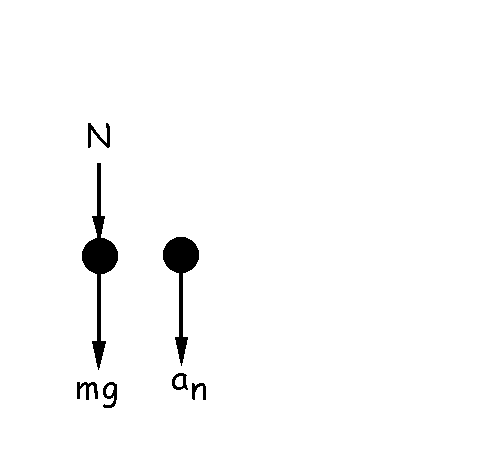
El punto crítico será el de la parte superior del bucle. En dicho punto la bola debe tener velocidad. Vamos a determinar cuál es la mínima velocidad con que puede llegar al punto más alto del bucle. Si aislamos la bola en ese punto tendremos el diagrama que se muestra en la figura. Obviamente, como la bola está describiendo un movimiento circular, estará sometida a la aceleración normal o centrípeta. Si aplicamos la segunda ley de Newton tendremos:

La velocidad será tanto menor cuanto menor sea la normal. El valor más bajo que puede tomar la normal es cero, ya que valores negativos implicarían un cambio de sentido que es imposible. Por tanto la mínima velocidad con que la bola puede llegar a la parte más alta del bucle es:

Ahora vamos a aplicar la conservación de la energía, entre el punto de partida, donde se suelta a la partícula desde el reposo a una altura h, y el punto más alto del bucle, donde la bola tiene velocidad v y está situada a una altura 2R. Nos queda: