Cuestion de Introducción (Magnitudes y Vectores)

Demostrar que el sistema de vectores F1=2i, F2=-i y F3=-i, aplicados en los puntos (0, 0, 0),

(0, 1, 0) y (0, 0, 1) respectivamente, se puede reducir a un par y determinar dicho par.

Mo=-j+k

Llamaremos a los puntos en los que están aplicados los vectores:

O=(0, 0, 0); A=(0, 1, 0); B=(0, 0, 1)

Para que el sistema de vectores pueda reducirse a un par se deberá verificar que la resultante sea nula:

R=S
F=F1+F2+F3=2i–i–i=0

Por tanto efectivamente, el sistema puede reducirse a un par. Dicho par será:

El vector F1 no da momento respecto del punto O porque está aplicado en él luego:

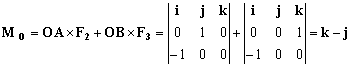
M0=-j+k