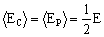E=EC+Ep; ![]()
En el movimiento armónico simple la aceleración puede expresarse como:
![]()
Entonces podemos reescribir la ecuación general del movimiento como:
![]() ⇒ mvdv+kxdx=0
⇒ mvdv+kxdx=0
que es una ecuación diferencial de primer orden. Por integración, esta ecuación diferencial nos conduce a:
![]()
El primer término de esa ecuación es la energía cinética de la partícula; el segundo término corresponde a la energía potencial. En consecuencia, la constante del segundo término es la energía total E, esto es:
E=EC+EP
Por lo tanto, la energía total de la partícula es constante durante el movimiento.
Los valores medios de las energías cinética y potencial del oscilador armónico simple son iguales: