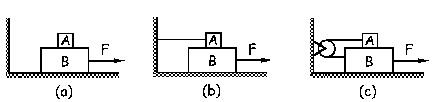
a) F=39.2 N
b) F=49 N
c) F=58.8 N
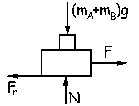 a) En cualquiera de los tres casos la velocidad del bloque B va a ser constante, luego su aceleración será nula. Tendremos siempre pues que la suma de todas las fuerzas aplicadas sobre el cuerpo debe ser nula. Aislamos el sistema completo y tendremos:
a) En cualquiera de los tres casos la velocidad del bloque B va a ser constante, luego su aceleración será nula. Tendremos siempre pues que la suma de todas las fuerzas aplicadas sobre el cuerpo debe ser nula. Aislamos el sistema completo y tendremos:
ΣFY=0 ⇒ N-(mAg+mBg)=0 ⇒ N=(mA+mB)g=(5+15) · 9.8=196 N
ΣFX=0 ⇒ F-Fr=0 ⇒ F=Fr=µN=0.2 · 196=39.2 N
F=39.2 N
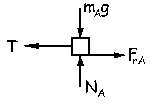 b) Ahora empezamos por aislar el bloque A. Para este bloque:
b) Ahora empezamos por aislar el bloque A. Para este bloque:
ΣFY=0 ⇒ NA-mAg=0 ⇒ NA=mAg=5·9.8=49 N
ΣFX=0 ⇒ FrA-T=0 ⇒ T=FrA=µNA=0.2·49=9.8 N
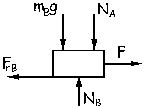 Y ahora aislamos el bloque B. Para este bloque:
Y ahora aislamos el bloque B. Para este bloque:
ΣFY=0 ⇒ NB-NA-mBg=0
NB=NA+mBg=49+15 · 9.8=196 N
ΣFX=0 ⇒ F-FrA-FrB=0
F=FrA+FrB=µNA+µNB=µ(NA+NB)=0.2(49+196)=49 N
F=49 N
c) Empezamos, como antes, por aislar el bloque A. No hace falta trazar el dibujo porque sería idéntico al del apartado b). Para este bloque:
ΣFY=0 ⇒ NA-mAg=0 ⇒ NA=mAg=5·9.8=49 N
ΣFX=0 ⇒ FrA-T=0 ⇒ T=FrA=µNA=0.2·49=9.8 N
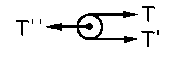 Ahora aislamos la polea. Si denominamos O a su centro geométrico y R a su radio tendremos:
Ahora aislamos la polea. Si denominamos O a su centro geométrico y R a su radio tendremos:
ΣMO=0 ⇒ TR-T’R=0 ⇒ T=T’=9.8 N
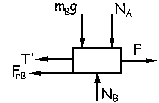 Por último aislamos el bloque B. Entonces:
Por último aislamos el bloque B. Entonces:
ΣFY=0 ⇒ NB-NA-mBg=0 ⇒ NB=NA+mBg=49+15·9.8=196 N
ΣFX=0 ⇒ F-FrA-FrB-T’=0
F=FrA+FrB+T’=µNA+µNB+T’==µ(NA+NB)+T’=0.2(49+196)+9.8=58.8 N
F=58.8 N