Cuestion de Gravitación

Un cometa describe una órbita elíptica alrededor del Sol. Se consideran dos puntos A y B de esa órbita, estando A más alejado del Sol que B. Comparar en A y en B los valores de las siguientes magnitudes asociadas al cometa: a) energía potencial; b) velocidad (en módulo); c) aceleración (en módulo); d) momento cinético con respecto al Sol.

 

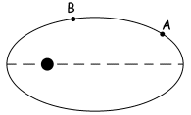
a) EPA > EPB
b) vA < vB
c) aA < aB
d) LA=LB

a) La energía potencial vale:

Tenemos que:

rA>rB

Por lo tanto, en módulo:

Pero como tiene signo negativo:

EPA>EPB

 

b) Entre los puntos A y B se debe conservar la energía total:

ETA=ETB ⇒ ECA+EPA=ECB+EPB

Hemos deducido del apartado anterior que:

EPA>EPB ⇒ ECA<ECB

Teniendo en cuenta la expresión de la energía cinética:

vA<vB

 

c) La única fuerza que existe es la de atracción gravitatoria, que vale:

Como se debe cumplir la segunda ley de Newton:

F=ma

Entonces:

Por tanto tendremos:

aA<aB

 

d) El momento angular o cinético respecto al Sol se conserva por ser un caso de fuerzas centrales. Entonces:

LA=LB