S=7.97 cm; β=2.14
En espejos esféricos el foco siempre está entre el centro de curvatura y el vértice y justo en la mitad. Por tanto:
R=2f=2·15=30 cm
Como el espejo es cóncavo su radio será negativo:
R=-30 cm
El hombre debe ver la imagen a 25 cm de él, pues es donde la verá mejor. Además dicha imagen debe estar derecha respecto del objeto, de modo que teniendo en cuenta la ecuación del aumento lateral:
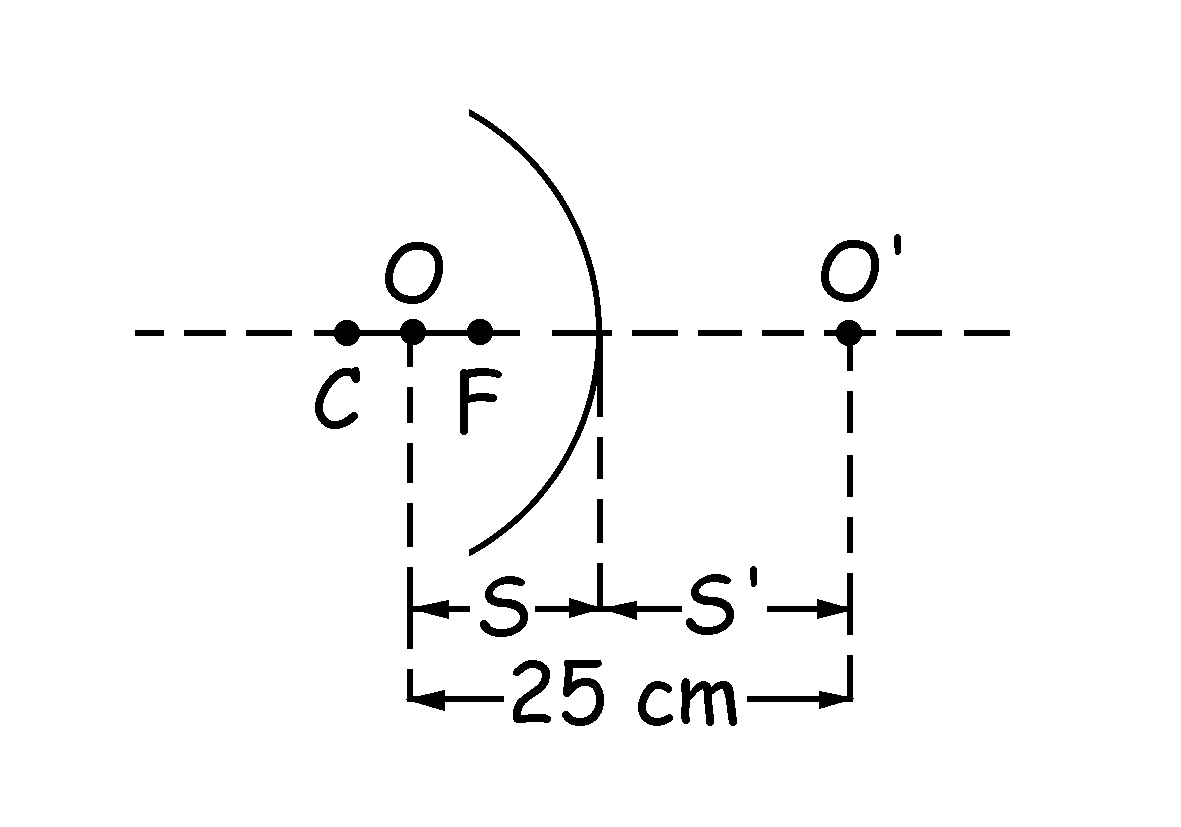Para que y e y’ tengan el mismo signo, y por tanto la imagen esté derecha respecto del objeto, el aumento lateral debe ser negativo, luego S y S’ tendrán distinto signo. El hombre está delante del espejo (distancia objeto negativa) luego su imagen estará detrás del espejo (distancia imagen positiva). En el gráfico tenemos un esquema de la situación. Aplicando la ecuación de los espejos:
-375+30S=-25S+S2 ⇒ S2-55S+375=0 ⇒ 
Tenemos que despreciar la primera solución, ya que es mayor de 25 cm, que es la distancia que separa objeto e imagen, y esta solución es físicamente imposible si tenemos en cuenta que están a ambos lados del espejo. La distancia objeto es por tanto:
S=7.97 cm
La distancia imagen correspondiente es:
S’=25-S=25-7.97=17.03 cm
Y por tanto el aumento lateral será:
β=2.14