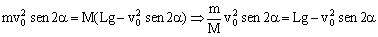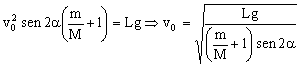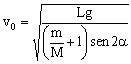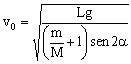
La cantidad de movimiento del sistema tabla-saltamontes (despreciaremos la masa del mosquito) en la dirección horizontal se conservará, ya que las únicas fuerzas que actúan sobre él son internas. Denominaremos v0 a la velocidad inicial del saltamontes, que forma un ángulo α con la horizontal. Inicialmente el sistema está en reposo (cantidad de movimiento nula), luego cuando el saltamontes salte la cantidad de movimiento del sistema debe ser nula. Eso implica que si el saltamontes salta hacia la izquierda con velocidad v0cosα la tabla se desplazará hacia la izquierda con velocidad v, de modo que:
mv0cosα=Mv ⇒
![]()
Cuando el saltamontes se desplace hacia la izquierda la tabla se moverá hacia la derecha. Llamaremos t al tiempo que el saltamontes está en el aire. El saltamontes recorre un espacio v0cosαt mientras que la tabla se desplaza en sentido contrario un espacio L-vt (recuérdese que en el eje horizontal el movimiento es rectilíneo y uniforme). Para que el saltamontes alcance al mosquito estos dos espacios deberán coincidir:
v0cosαt=L-vt
Además, el saltamontes realiza un movimiento parabólico. En el eje vertical la velocidad inicial es v0senα. El tiempo que el saltamontes está en el aire será el doble del que tarda en llegar a la altura máxima. Sabiendo que en el eje Y el movimiento es uniformemente acelerado, con aceleración la de la gravedad, ese tiempo t es:
![]()
Sustituimos este tiempo en la ecuación que nos relaciona los espacios:
v0cosαt=L-vt ⇒
![]()
![]()
![]()
Y sustituimos esta ecuación en la expresión de v0:
![]()
Teniendo en cuenta que:
2senαcosα=sen2α ⇒
![]()