a) ΣMCM=0 ⇒ Tcos45º · 2sen30º+Tsen45º · 2cos30º+Ox 2sen30º-Oy · 2cos30º=0;
ΣMO=0 ⇒ Tcos45º · 4sen30º+Tsen45º · 4cos30º-mg2cos30º=0
b) T=219,66 N; Ox=155,32 N; Oy=334,68 N
c) α=3,183 rad/s2
Problema de Dinámica de los Sistemas de Partículas
Aparece en la convocatoria ENE2021
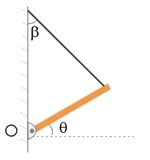
Una barra homogénea de 4 m de longitud y masa 50 kg está sujeta a una pared mediante una articulación sin rozamiento en el punto O y por una cuerda desde el otro extremo, como se ve en la figura. Sabiendo que θ=30º y β=45º: a) dibujar las fuerzas que actúan sobre la barra y expresar las ecuaciones para que el sistema esté en equilibrio; b) calcular las componentes de la reacción en la articulación y la tensión en la cuerda en las condiciones del apartado a); c) en un momento dado se suelta la cuerda y la barra cae. Determinar la aceleración angular que adquiere la barra inmediatamente después de cortar la cuerda.
