a) Δl1=10.98 mm; Δl2=3.49 mm
b) EFe=2.211·1011 N/m2
c) ν’=48.07 s-1
d) hilo 1: nnodos=9, xnodos=0, 0.5, 1.0, 1.5, 1.8, 2.1, 2.4, 2.7, 3.0 m
hilo 2: nnodos=2, xnodos=0, 3.0 m
Problema de Movimiento Ondulatorio
Aparece en la convocatoria SEP2003
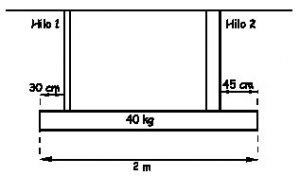
Una barra rígida de 2 m de longitud y 40 kg de masa está sujeta por dos hilos de cobre de la misma longitud, l=3 m, y de diámetros d1=1 mm y d2=2 mm, como se muestra en la figura. a) Determinar los incrementos de longitud de cada hilo (módulo de Young del cobre ECu=6·1010 N/m2). b) El hilo de menor diámetro se reemplaza por otro formado por dos materiales, cada uno de longitud 1.5 m. La primera mitad sigue siendo de cobre, y la segunda mitad del hilo se ha sustituido por una aleación de hierro, ambos con el mismo diámetro d1=1 mm. Con la misma disposición de hilos que en el apartado a), se observa que el incremento de longitud del hilo más fino (el formado por la unión del cobre más la aleación de hierro) es el doble que el incremento de longitud del hilo más grueso (sólo de cobre). Determinar el módulo de Young de la aleación de hierro. c) A continuación se monta cada hilo de la situación b) por separado y se tensan con sendos pesos de 80 kg. Se producen perturbaciones en ambos hilos generando ondas transversales estacionarias en los hilos. Si las densidades de los dos materiales son ρCu=3000 kg/m3 y ρaleación=8330 kg/m3, determinar la frecuencia de vibración más baja de las ondas transversales producidas en cada hilo, de modo que el punto de unión entre los dos materiales sea un nodo; d) determinar el número de nodos que se producen en cada hilo y las posiciones exactas de los mismos. Se puede considerar despreciable el peso de los hilos.