a) K = 9’8.108 N/m2
b) ρ = 128,65 kg/m3
c) 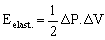
d) (Eelast)exp = 980 J
e) v1 = 1490,4 m/s
f) 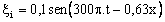 ;
;  ;
; 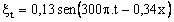
g) ν’’ = 156,58 Hz
Problema de Movimiento Ondulatorio
Aparece en la convocatoria SEP2009
Una bolsa de gas se encuentra en la superficie del mar ocupando un volumen inicial de 2000 litros. Se sumerge a 100 m de profundidad, experimentando por la presión del mar un cambio de volumen de 2 litros.
a) Determinar el módulo de elasticidad en volumen de este gas.
b) La temperatura del mar a esa profundidad de 100 m es de -70 oC, mientras que en la superficie del mar es 0 oC. Si la velocidad de propagación de las ondas sonoras en el gas en la superficie del mar es de 3200 m/s, determinar la densidad del gas a los 100 m de profundidad.
c) A partir de la energía potencial elástica deducida para un paralepípedo sometido a esfuerzos en las tres direcciones del espacio, deducir la expresión de la energía potencial elástica de éste gas comprimido.
d) Calcular el valor de dicha energía potencial elástica en la situación de la experiencia.
e) Un pulso de ondas sonoras de frecuencia 150 Hz se propaga desde el mar a la bolsa de gas. El coeficiente de reflexión en el proceso es R=0,3. Determinar la velocidad de propagación de la onda sonora en el agua del mar en esas condiciones (a los 100 m de profundidad).
f) Escribir las ecuaciones de las ondas incidente, reflejada y transmitida, suponiendo una amplitud incidente de 0,1 m.
g) La onda anterior la ha emitido una ballena que se mueve a una velocidad de 22 m/s avanzando hacia la bolsa. Si la bolsa se ve arrastrada en ese momento por una corriente marina que tiene una velocidad de 10 m/s y avanza contra el sentido de movimiento de la ballena, ¿qué frecuencia percibe la ballena de la onda que rebota sobre la bolsa? (considérese en este apartado que la bolsa de gas actúa sin más como una superficie reflectante de las ondas que inciden sobre ella).
Datos: densidad del agua del mar ρ=1.03 kg/l