a) kC=3040 N/m
b) y=0.25sen(8.718t+0.812) ó y=0.25cos(8.718t-0.759)
c) vmáx=2.179 m/s; amáx=19 m/s2
d) 28 oscilaciones
e) y=0.25e-0.278tsen(8.713t+1.539) ó y=0.25e-0.278tcos(8.713t-0.0319)
Problema de Movimiento Oscilatorio
Aparece en la convocatoria FEB2012
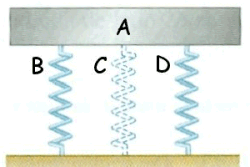
La plataforma A de 50 kg está unida a los muelles B y D, de constante k=1900 N/m cada uno.
Se desea que la frecuencia de vibración de la plataforma no varíe cuando sobre ella se deposite un bloque de 40 kg, por lo que se añade un tercer muelle C. a) Hallar la constante de éste tercer muelle; b) el sistema completo (tres muelles, plataforma y bloque) oscila con una amplitud de 25 cm. Determina la ecuación del movimiento si consideramos que en el inicio de tiempos la velocidad es de 1.5 m/s; c) calcula la velocidad y aceleración máximas; d) a continuación se ejerce sobre el sistema una fuerza de rozamiento proporcional a la velocidad, siendo la constante de proporcionalidad 50 Ns/m. Determina el número de oscilaciones que tienen que pasar para que el sistema se considere parado, si suponemos que la oscilación inicial es de 25 cm de amplitud y lo podemos considerar en reposo cuando la amplitud de las oscilaciones es inferior a 1 mm; e) calcula en este caso la ecuación del movimiento, considerando que la amplitud inicial es A0=25 cm y que el origen de tiempos comienza cuando la velocidad es nula.