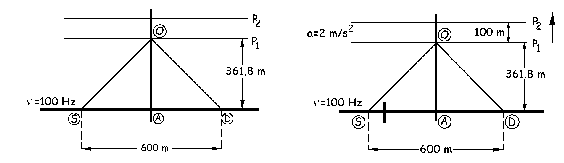Una experiencia consiste en una fuente S y un detector D separados una distancia de 600 m, equidistantes de un eje transversal AO. La fuente S emite ondas sonoras (v=340 m/s) de frecuencia ν=100 Hz. a) En una primera parte de la experiencia, las ondas que salen de S llegan a D por dos caminos diferentes: directamente, y después de reflejarse en una pared P. Esta se sitúa primero en una posición P1 y después en una posición diferente P2, para las cuales se obtiene en D respectivas situaciones de mínimo de intensidad, habiéndose observado además entre ambas posiciones 100 situaciones de máximo de intensidad. Si la distancia entre la pared en la posición P1 y la recta SD es de 361.8 m, ¿cuál es el espacio entre las posiciones P1 y P2 de la pared? b) En una segunda parte de la experiencia se elimina la onda directa que llega al detector, colocando un obstáculo en el camino SD, de forma que a D sólo llegan ondas después de rebotar en la pared P. Se quiere además que la pared alcance diferentes posiciones, para lo cual se da a la pared un movimiento uniformemente acelerado con a=2 m/s2. En estas condiciones, en una posición P1 de la pared se obtiene en D una frecuencia de ν´=92.3 Hz. Calcular la frecuencia ν1 percibida por el observador O colocado en el centro de la pared en esta posición P1. Si para una posición P2 se tiene que P1P2=100 m, calcular la frecuencia ν2 observada por O en la nueva posición P2.
; superficie de la elipse: S=πab.
