Problemas

Dos lentes convergentes alineadas sobre un eje común, la primera de 20 cm de focal y la segunda el doble, están separadas por 60 cm. Introducimos entre ambas una tercera lente convergente de focal desconocida. a) Sabiendo que la imagen de un objeto situado 12 cm a la izquierda de la primera lente es real y está a 60 cm de la última lente, y que el aumento lateral del conjunto es (-15/8), calcula la focal de la tercera lente y su posición entre las otras dos; b) la primera lente está formada por la yuxtaposición de dos lentes, una de ellas biconvexa de radios iguales e índice de refracción 1.35 y la otra cóncavo-convexa de focal -26.67 cm y radios en relación 1 a 2. ¿Cuál es el índice de refracción de la segunda lente y cuáles los radios de ambas lentes? c) Si sustituimos la lente de focal 40 cm por un espejo que del mismo objeto del apartado a) da una imagen real a 40 cm del mismo, ¿cuál es su radio? ¿Es cóncavo o convexo?

Problema de Óptica geométrica. Aparece en la convocatoria de SEP2004.

Dos lentes delgadas convergentes de distancias focales f₁=10 cm y f₂=15 cm distan entre sí 5 cm. Hallar la posición de la imagen de un objeto situado a 30 cm de la primera lente mediante los dos métodos siguientes: a) un cálculo lente a lente; b) considerar la lente compuesta como una lente gruesa.

Problema de Óptica geométrica.

Dos moles de un gas ideal biatómico (ϒ=1.4) describen el ciclo termodinámico reversible ABCA. En A la presión es de 5 atm y la temperatura de 27 ºC, mediante una expansión isobárica duplica su volumen en B, de B pasa a C mediante una expansión adiabática y después desde C mediante una compresión isotérmica vuelve a A. Calcular: a) el volumen y la temperatura del gas en B y C; b) el trabajo realizado por el gas y la variación de energía interna en las transformaciones AB, BC y CA; c) la variación de entropía en las transformaciones AB, BC y CA; d) el rendimiento del ciclo.
R=0.082 atml/molK; 1 atm=101324.72 N/m².

Problema de Entropia y Segundo Principio de la Termodinámica. Aparece en la convocatoria de JUN2006.

Dos moles de un gas ideal monoatómico inicialmente a 1 atm y 300 K realizan el siguiente ciclo, cuyas etapas son todas reversibles: 1) Compresión isotérmica hasta 2 atm, 2) Aumento isobárico de la T hasta 400K y 3) Retorno al estado inicial por el camino P=a+bT, siendo a y b constantes.
a) Dibuja esquemáticamente el ciclo sobre un diagrama P-T.
b) Calcula P, V y T de cada uno de los estados.
c) Calcula las variaciones numéricas ΔU y ΔS para cada etapa del ciclo.
d) En algún punto del último proceso la presión vale 1.5 atm ¿Cuánto vale entonces la temperatura?
(Cv para un gas ideal monoatómico = 3/2 R).

Problema de Entropia y Segundo Principio de la Termodinámica. Aparece en la convocatoria de JUN2009.

Dos movimientos vibratorios perpendiculares entre sí tienen el mismo período T, la misma amplitud A=2 y una diferencia de fase igual a . Calcular gráfica y analíticamente la oscilación que resulta.

Problema de Movimiento Oscilatorio.

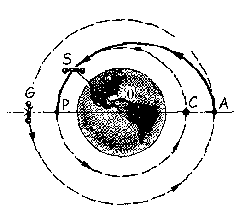
Dos naves espaciales, Galileo (G) y Sócrates (S), se encuentran en dos órbitas circulares en torno a la Tierra, moviéndose con velocidades de 7072.84 m/s y 7561.18 m/s, ambas en sentido horario. Se quiere hacer que la nave Galileo se acople con Sócrates justo en el punto P. Para ello, Galileo parte del punto G y Sócrates del punto S en un cierto instante. Al llegar al punto A, Galileo disminuirá su velocidad para situarse en una órbita elíptica de transición (elipse AP), y posteriormente volverá a disminuirla en el punto P acoplándose con Sócrates. Determinar: a) incremento de velocidad que debe producirse en la nave Galileo en el punto A para pasar de la primera órbita circular a la órbita elíptica de transición; b) incremento de velocidad que debe producirse en dicho vehículo en el punto P para transferirlo a la segunda órbita circular; c) velocidad areolar del vehículo Galileo en la primera órbita circular; d) período de la órbita de transición; e) el ángulo q que define la posición a ocupar por el vehículo Sócrates al inicio de la maniobra para que el acoplamiento se produzca en el punto indicado (despreciar el tiempo invertido en los incrementos de velocidad).
Datos: masa de la Tierra M=6·10²⁴ kg; radio de la Tierra R=6370 km; constante de gravitación universal G=6.67·10^-11 Nm²/kg².

Problema de Gravitación. Aparece en la convocatoria de JUL2001.

Dos objetos se encuentran en reposo sobre una superficie sin rozamiento. El objeto 1 tiene una masa mayor que el objeto 2. Cuando se aplica una fuerza al objeto 1 éste se acelera a lo largo de un desplazamiento Δx. Se deja de ejercer la fuerza sobre el objeto 1 y se aplica al objeto 2. Una vez que el objeto 2 se ha acelerado a lo largo del mismo desplazamiento Δx, cuál de las siguientes relaciones es cierta: a) p₁ < p₂; b) p₁=p₂; c) p₁ > p₂; d) K₁ < K₂; e) K₁=K₂; f) K₁ > K₂ (p=cantidad de movimiento, K=energía cinética).

Cuestion de Trabajo y Energía.

Dos partículas de masas m₁=2 kg y m₂=5 kg pueden moverse libremente y sin fricción sobre un alambre guía horizontal. Si la partícula m₁ se mueve con una velocidad v₁=17 m/s y alcanza a la m₂, que tiene un resorte ideal sin masa de constante k=4480 N/m sujeto por el lado por el que se aproxima m₁, que se mueve en el mismo sentido con una velocidad v₂=3 m/s (ver figura), determinar: a) la máxima compresión del resorte cuando colisionan las dos partículas; b) las velocidades finales de las mismas.

Problema de Dinámica de los Sistemas de Partículas.

Dos piezas soportan el peso P que está apenas en contacto con el muelle elástico sin deformar, de constante k y peso despreciable. Si se retiran súbitamente las dos piezas, determinar la velocidad máxima alcanzada por el peso, la fuerza máxima transmitida al suelo por el muelle, y la deformación máxima del muelle.

Problema de Trabajo y Energía.

Dos placas A y B de 50 kg de masa cada una se colocan sobre un plano inclinado 15^o como muestra la figura. Si el coeficiente de rozamiento entre las placas es de 0.1 y entre la placa A y el plano inclinado es 0.15, determinar la aceleración de cada placa.

Problema de Dinámica de la Partícula.