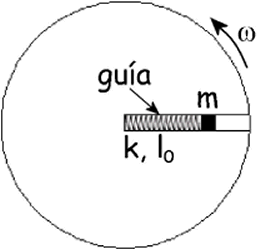
El sistema mostrado en la figura (visto desde arriba) consta de una masa m=200 g unida a un muelle (k=1 kN/m) que puede estirarse a lo largo de la guía en la que está contenido. Todo el sistema descansa en una plataforma horizontal capaz de girar. Se considera despreciable el rozamiento de la masa con la plataforma y con las paredes de la guía. La longitud en reposo del muelle es l0=35 cm.
A continuación se imprime una velocidad angular ω constante a la plataforma giratoria, lo que produce que el muelle se estire una cierta cantidad.
a) Realiza el diagrama del cuerpo libre de la masa en la situación en la que la plataforma está en reposo.
b) Realiza el diagrama del cuerpo libre de la masa cuando la plataforma está girando con velocidad angular ω. ¿Cuál es la aceleración de la masa en esta situación?
c) Determina el estiramiento del muelle cuando ω=6 r.p.s. A continuación se desplaza la masa m una cantidad adicional x a lo largo de la guía.
d) Teniendo en cuenta la expresión de la aceleración absoluta de una partícula:
a=a0+αxOP+ωx(ωxOP)+2ωxvrel+arel
discútase el movimiento absoluto ulterior de la masa, considerando el posible movimiento relativo de dicha masa y el movimiento del sistema en el que está contenida.
e) Determina el valor del periodo de las oscilaciones de este sistema cuando ω=6 rps.
. Las bolitas A y B de igual masa m=60 g resbalan sin rozamiento a lo largo del tubo. Si las longitudes de los resortes R1 y R2, sin deformar, son 50 cm y 60 cm, y sus constantes elásticas 150 N/m y 160 N/m respectivamente, calcule el aumento de longitud de cada resorte y las tensiones en cada uno de ellos.
