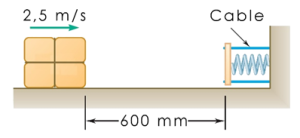
Cuestion de Dinámica de la Partícula. Aparece en la convocatoria de ENE2024.
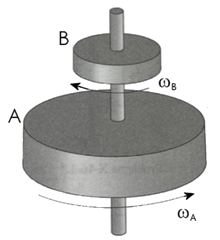
Cuestion de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2024.
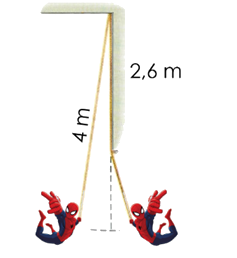
Cuestion de Movimiento Oscilatorio. Aparece en la convocatoria de ENE2024.
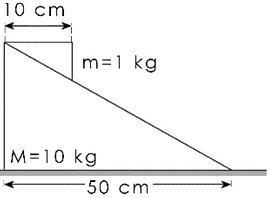
Cuestion de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2024.
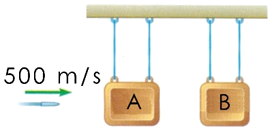
Cuestion de Dinámica de los Sistemas de Partículas. Aparece en la convocatoria de ENE2024.
Cuestion de Trabajo y Energía. Aparece en la convocatoria de ENE2024.
Cuestion de Movimiento Oscilatorio. Aparece en la convocatoria de ENE2024.
Cuestion de Dinámica de los Sistemas de Partículas. Aparece en la convocatoria de ENE2024.