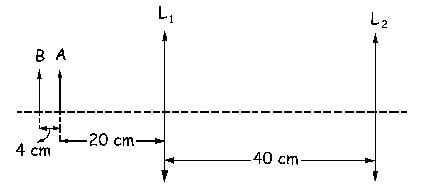
a) Una lente convergente de 12 cm de distancia focal está formada a su vez por dos lentes convergentes convexo-cóncavas yuxtapuestas, de modo que las superficies en contacto tienen el mismo radio. Una de las lentes tiene un índice de refracción de 1.2 y los radios de curvatura de sus caras están en relación 1 a 2; la otra tiene un índice de refracción de 1.4 y los radios de curvatura de sus caras están en la relación 2 a 3. Determinar los radios de curvatura de las caras de dichas lentes. b) Un sistema óptico está formado por dos lentes delgadas convergentes L1 y L2, de 12 cm y 8 cm de focal respectivamente, situadas en este orden sobre un eje óptico, y distantes entre sí 40 cm. Delante de L1 se encuentran dos objetos idénticos verticales, A y B, separados por 4 cm, y distantes A de L1 20 cm (ver figura). Determinar la relación entre los tamaños de las dos imágenes; c) a continuación se desplaza L2 hacia la izquierda hasta quedar en contacto con L1. Encontrar la posición de las nuevas imágenes y su relación de alturas.