Problema

Determine la resultante de las dos ondas:

y₁=6sen(100πt)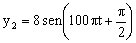

Problema de Interferencias.

Una lente convergente, cuya distancia focal es f=10 cm, fue cortada al medio y las mitades fueron desplazadas una distancia d=0.5 mm (lente doble). Calcular el número de franjas de interferencia en la pantalla, situada detrás de la lente a una distancia de 60 cm, si delante de la lente existe una fuente puntual de luz monocromática (λ=500 nm) alejada de ella 15 cm.

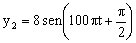
Problema de Interferencias.

Por reflexión normal en un obstáculo indeformable de una onda plana armónica y progresiva se producen ondas estacionarias que, prescindiendo de la absorción, vienen dadas por la ecuación:

estando x e y en cm y t en s. Determinar: a) las ondas incidente y reflejada; b) posición y distancia entre nodos; c) posición y distancia entre vientres (antinodos); d) velocidad de una partícula en la posición x=1.5 cm en el instante t=1 s.

Problema de Interferencias.

a) ¿A qué distancia deben estar entre sí dos objetos en la Luna para que puedan ser resueltos por el ojo sin la ayuda de ningún instrumento? Considerar que el diámetro de la pupila del ojo es de 5 mm, la longitud de onda de la luz es 600 nm y la distancia a la Luna es de 380000 km. b) ¿A qué distancia deben estar los objetos en la Luna para que puedan ser resueltos mediante un telescopio que tiene un espejo de 5 m de diámetro?

Problema de Difracción.

La lente convergente gruesa de la figura tiene un índice de refracción de 1.5 y sus radios de curvatura son r₁=20 mm y r₂=30 mm, siendo su espesor 30 mm. Hallar las posiciones F, F´, H y H´. Situar el punto imagen de un punto objeto S que está situado 80 mm a la izquierda del primer vértice y 10 mm por encima del eje.

Problema de Óptica geométrica.

Un sistema óptico consta de dos lentes con distancias focales iguales en magnitud absoluta. Una de las lentes es convergente y la otra divergente. Las lentes están instaladas en el mismo eje, a cierta distancia la una de la otra. Se sabe que al cambiar las lentes, la imagen real de la Luna, proyectada por el sistema se desplaza en l=20 cm. Encontrar la distancia focal de cada una de las lentes.

Problema de Óptica geométrica.

Se dispone de dos lentes delgadas alineadas en un eje óptico y distantes entre sí 40 cm, la primera de ellas está formada por la yuxtaposición de una biconvexa, de radios iguales (r=30 cm) e índice de refracción 1.5 y otra cóncavo-convexa de radios 30 cm y 20 cm respectivamente e índice de refracción 1.4. La segunda lente es una lente convergente de focal 10 cm. Calcular: a) la focal de la primera lente. b) la posición, carácter y tamaño de la imagen de un objeto, inclinado 30^o respecto al eje óptico, de 2.31 cm de longitud y cuya base está situada a 90 cm a la izquierda de la primera lente.
Segunda parte: Considérese un sistema óptico centrado formado por dos lentes delgadas separadas una distancia d=9 cm. Un punto O situado a 26 cm a la izquierda del plano principal objeto del sistema óptico compuesto equivalente (S.O.C.) tiene su imagen O´ situada a 16.25 cm a la derecha del plano principal imagen del S.O.C. Se sabe también que la imagen de la primera lente dada por el sistema está situada a 15 cm a la izquierda del plano principal imagen del S.O.C. Calcular: c) las focales f₁ y f₂ de las lentes y dibújense las posiciones de los planos principales del sistema respecto a las lentes.
(NOTA: distancia focal imagen del S.O.C. ; distancias de las lentes a los planos principales: )

Problema de Óptica geométrica.

600 g de perdigones de plomo se calientan a 100 ^oC y se colocan en un bote de aluminio de 200 g de masa que contiene 500 g de agua inicialmente a 17.3 ^oC. El calor específico del aluminio del bote es 0.900 kJ/kgK. La temperatura final del sistema es de 20.0 ^oC. ¿Cuál es el calor específico del plomo? Calor específico del agua: 4.18 kJ/kgK.

Problema de Calor y Primer Principio de la Termodinámica.

Calcular la velocidad cuadrática media de una molécula de hidrógeno a la temperatura de 20 ^oC, en un recinto donde la presión es 70 cm de Hg. Peso molecular del hidrógeno: 2.016 g/mol; 1 atm=101324.72 N/m².

Problema de Teoría Cinética de los Gases.

Un mol de un gas perfecto se expansiona isotérmicamente a 27 ^oC desde un volumen inicial de 2 l hasta uno final de 8 l. Calcular la variación de energía interna, de entalpía y de entropía. R=2 cal/molK.

Problema de Entropia y Segundo Principio de la Termodinámica.