Problema

Cuando la barra delgada de 10 kg está en posición horizontal se encuentra en reposo y con el resorte sin deformar. Determinar: a) la constante del resorte si en el movimiento posterior la barra se detiene momentáneamente cuando ha rotado 90º en el sentido de las agujas del reloj; b) la aceleración angular de la barra en ese instante; c) las reacciones en el pasador en ese momento. Si no has podido resolver el primer apartado, supón k=42 N/m.

Momento de inercia  de una barra respecto de un eje que pasa por su centro de masas:

 

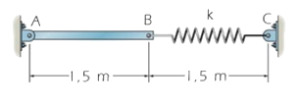
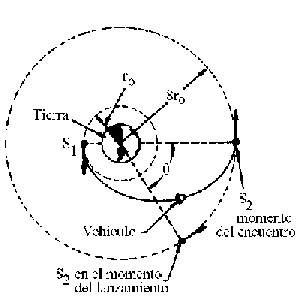
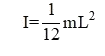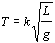Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2022.

¿Cuál es la masa en gramos de un cuerpo que pesa exactamente 1 dina en un punto en el que g=9,81 m/s²? ¿Cuál es la masa de un cuerpo que pesa 1 N en ese punto? ¿Cuál es la masa en slug de un cuerpo que pesa 1 libra en ese punto

Problema de Introducción (Magnitudes y Vectores).

Utilizando un sistema que tenga como unidades fundamentales la presión de 1 kp/cm ², la densidad absoluta del mercurio a 0^o C 13.6 g/cm³ y la aceleración de la gravedad 9.8 m/s², determinar la ecuación dimensional del tiempo y el valor de su unidad en segundos.

Problema de Introducción (Magnitudes y Vectores).

Un hombre cruza transversalmente una calle entre los puntos A y B de la figura, separados 12 m, con una velocidad de 2 m/s. Al hacerlo es iluminado por un farol L, situado a 1 m de B, con lo que se proyecta la sombra del hombre sobre la pared de partida. a) ¿A qué velocidad se mueve la sombra cuando el hombre está a 5 m de A? b) ¿Dónde está el hombre cuando la sombra se mueve a la misma velocidad con la que él anda?

Problema de Cinemática de la Partícula.

El brazo ranurado pivota en O y gira en sentido contrario a las agujas del reloj con velocidad angular constante ω en torno a la leva circular que es fija y está montada excéntricamente. Determinar la velocidad v y la aceleración a del vástago en la posición θ=π/2. El vástago tiene diámetro despreciable y se mantiene en contacto con la leva.

Problema de Cinemática de la Partícula.

Un satélite viaja inicialmente en una órbita circular a 640 km sobre la superficie de la Tierra y su masa es 220 kg. a) Determinar su velocidad y su período. b) Por diversas razones, el satélite pierde energía mecánica a un ritmo (en promedio) de 1.4·10⁵ J por cada revolución orbital completa. Adoptando la aproximación razonable de que la trayectoria es una circunferencia cuyo radio disminuye lentamente, determinar su distancia a la superficie de la Tierra, su rapidez y su período al final de 1500 revoluciones orbitales; c) ¿cuál es la magnitud de la fuerza retardadora media?

Problema de Gravitación.

Una nave espacial describe una órbita circular de radio r₀ a una velocidad v₀, en torno a un cuerpo celeste indeterminado de centro O. Cuando se encienden los motores de la nave, su velocidad aumenta de v₀ a αv₀ describiendo entonces una órbita elíptica. Demostrar que en esta nueva órbita la distancia máxima alcanzada por la nave depende únicamente de r₀ y α, y expresar el cociente r_máxima/r₀ en función de α.

Problema de Gravitación.

Un camión de reparto hace los siguientes desplazamientos sucesivos: 1.37 km al suroeste, 0.85 km al norte y 2.12 km en dirección N 17^o O. Determinar el módulo y la dirección del desplazamiento resultante.

Problema de Introducción (Magnitudes y Vectores).

Siendo A=2t²i+2tj+3k, B=(t+2) i+t²j+2tk, vectores funciones de la variable escalar t, φ=4t²+t y b=2, determinar: a) ; b) ; c) ; d) ; e) ; f) .

Problema de Introducción (Magnitudes y Vectores).

Un bote de vela está bordeando a barlovento en dirección Nordeste con viento del Norte. La corredera registra una velocidad del casco de 6.5 nudos. El axiómetro (cordel ligero atado al aparejo) indica que la dirección aparente del viento forma 35^o con el eje del bote. ¿Cuál es la verdadera velocidad del viento v_w?

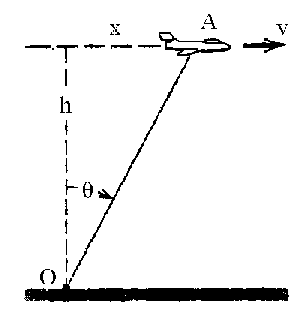
Problema de Cinemática de la Partícula.