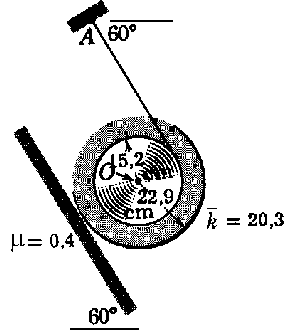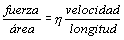Problema de Dinámica del Sólido Rígido.
Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de FEB2012.
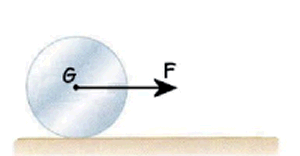
Problema de Trabajo y Energía. Aparece en la convocatoria de FEB2016.
Problema de Entropia y Segundo Principio de la Termodinámica. Aparece en la convocatoria de JUN2000.