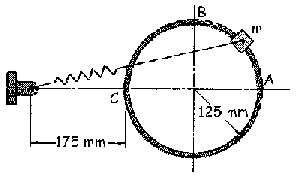
Una deslizadera de 1.5 kg está unida a un muelle y desliza sin rozamiento a lo largo de una barra circular que se encuentra en el plano horizontal. El muelle está sin deformar cuando la deslizadera está en C y su constante es de 400 N/m. a) Si la deslizadera se deja en reposo en B, determinar su velocidad cuando pasa por el punto C; b) se deja a continuación la deslizadera en el punto A en reposo. Determinar la componente horizontal de la fuerza ejercida por la barra sobre la deslizadera cuando la misma pasa por el punto B, y comprobar que dicha componente no depende de la masa; c) determinar en esa posición la aceleración de la deslizadera; d) a continuación, se sitúa todo el sistema en un plano vertical, de modo que el punto más alto de la trayectoria sea el punto A. Si se suelta la deslizadera desde el reposo en el punto A, determinar la aceleración de la deslizadera y la reacción de la barra sobre ésta cuando pasa por el punto B.