Tenemos un sistema formado por tres elementos: una varilla de 10 cm de longitud e índice de refracción 1.5 con sus extremos tallados y pulidos en forma de superficies esféricas convexas de radios 20 y 30 cm, una lente convergente de 10 cm de focal y un espejo convexo de radio 30 cm, dispuestos en este orden. a) Un objeto se sitúa 10 cm a la izquierda de la varilla. Si la distancia entre la varilla y la lente es de 20 cm, ¿a qué distancia estará la lente del espejo para que la imagen final sea virtual y se situé a 10 cm del espejo? b) ¿Cuál será el aumento total del sistema? c) Si sustituimos la lente convergente por una divergente de la misma focal, ¿dónde estará la imagen, cuál será su carácter y cuál será el aumento lateral del sistema? d) La nueva lente divergente es la yuxtaposición de dos lentes, una biconvexa de índice de refracción 1.5 y otra bicóncava de índice de refracción 1.6, de radios iguales. ¿Cuál es ese radio?
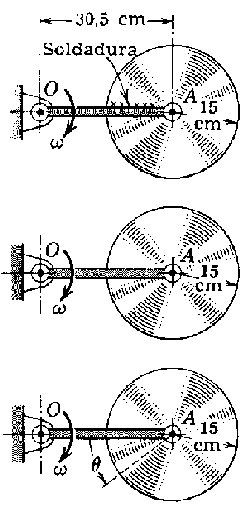
 . Calcular el momento cinético respecto al punto O del disco en cada caso.
. Calcular el momento cinético respecto al punto O del disco en cada caso.