Problema de Introducción (Magnitudes y Vectores).
Problema de Introducción (Magnitudes y Vectores).
Hallar un vector de módulo 3 y que sea paralelo al vector suma de: a=i+2j+k; b=2i–j+k; c=i–j+2k
Problema de Introducción (Magnitudes y Vectores).
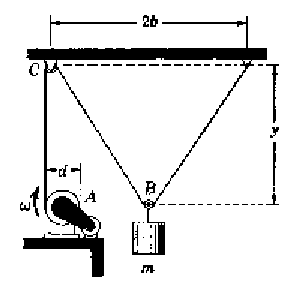
Problema de Dinámica de la Partícula.