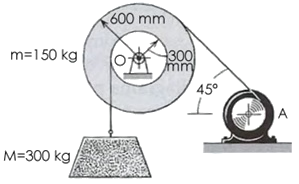
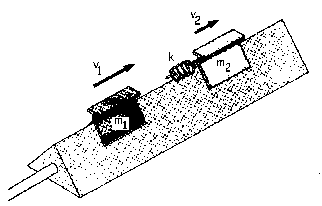
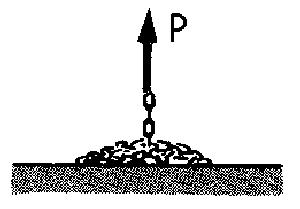
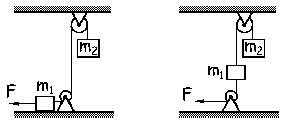Problema de Dinámica de los Sistemas de Partículas. Aparece en la convocatoria de FEB2021.
Cuestion de Dinámica de los Sistemas de Partículas.
Cuestion de Dinámica de los Sistemas de Partículas.
Problema de Dinámica de los Sistemas de Partículas.
Cuestion de Dinámica de los Sistemas de Partículas.
Problema de Dinámica de los Sistemas de Partículas.
Cuestion de Dinámica de los Sistemas de Partículas.