Problema de Dinámica del Sólido Rígido.
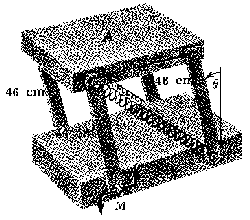
Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2009.
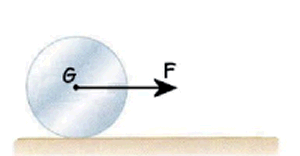
Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2018.
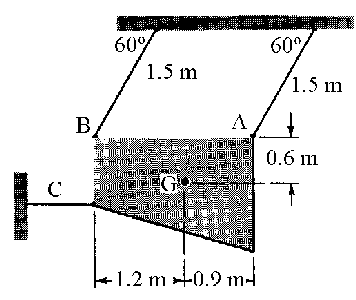
Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de FEB2012.
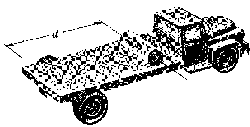
Problema de Dinámica del Sólido Rígido.
Problema de Dinámica del Sólido Rígido.
Demuestre que la cantidad de movimiento de un sólido respecto al centro de masas es nula.
Cuestion de Dinámica del Sólido Rígido.
Cuestion de Dinámica del Sólido Rígido.