Un objeto, por ejemplo un cometa recientemente descubierto, entra en el sistema solar y en su recorrido pasa alrededor del Sol. ¿Cómo podremos averiguar si dicho objeto regresará muchos años después o si nunca retornará? Cuestion de Gravitación.
Demostrar que la energía total de un satélite que describe una órbita circular es igual a la mitad de su energía potencial. Cuestion de Gravitación.
Un satélite de 4000 kg describe una órbita circular de 7000 km de radio alrededor de la Tierra. a) Al cabo de algún tiempo, como consecuencia de la fricción atmosférica, la órbita se reduce a otra circular de 6600 km. Calcular los cambios que experimenta la velocidad, la velocidad angular, el período de revolución y las energías cinética, potencial y total. b) Suponiendo que la resistencia del aire sobre el satélite represente una fuerza promedio de 2 N, estimar el tiempo necesario para la mencionada reducción del radio orbital. c) Hacer una estimación del número de vueltas que ejecuta el satélite durante ese tiempo. Problema de Gravitación.
Una nave espacial recorre una órbita circular a 3200 km sobre la superficie terrestre. Para regresar a la Tierra reduce su velocidad a un valor v0=5400 m/s e inicia de este modo una trayectoria elíptica. Determinar el valor de θ que define el punto B donde tiene lugar el amerizaje. Problema de Gravitación.
Suponer que la Tierra es una esfera de masa uniforme y que se ha taladrado un agujero de pequeño diámetro desde su superficie hasta su centro. a) ¿Cuánto trabajo se necesitaría para trasladar un objeto pequeño de masa m desde el centro de la Tierra a su superficie? b) Si se dejase caer el objeto por la abertura del agujero en la superficie terrestre, ¿con qué velocidad llegaría al centro? Cuestion de Gravitación.
Un cohete viaja de la Tierra a la Luna a lo largo de la línea recta que une sus centros. ¿A qué distancia la fuerza FTC que ejerce la Tierra sobre el cohete es igual y opuesta a la fuerza FLC que ejerce la Luna sobre el cohete? Masa de la Luna: ML=7.35·1022 kg; masa de la Tierra: MT=5.97·1024 kg; radio de la órbita de la Luna alrededor de la Tierra: rTL=3.84·108 m. Cuestion de Gravitación.
Un cometa de masa M se observa a una distancia de 1011 m del Sol viajando hacia él a una velocidad de 5.16·104 m/s haciendo un ángulo de 45o con el radio vector del Sol. Obtener: a) su energía total y su momento angular; b) la ecuación de la órbita; c) la distancia de mayor cercanía al Sol. Problema de Gravitación.
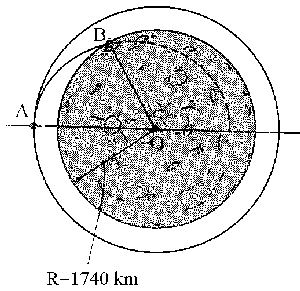
Después de concluir su misión de exploración en la Luna, los dos astronautas que formaron la tripulación del módulo de excursión lunar Apolo (LEM) se reunirían con el módulo de comando que había permanecido en una órbita circular alrededor de la Luna. Antes de su regreso a la Tierra, los astronautas pondrían su nave en una posición adecuada, de modo que el LEM se colocaría hacia la parte posterior de ésta. Cuando el módulo de comando pasara por A, el LEM se dejaría a la deriva, para estrellarse sobre la superficie de la Luna en el punto B. Sabiendo que el módulo de comando se encontraba en una órbita alrededor de la Luna a una altitud de 120 km, y que el ángulo AOB fue de 50o, determínese la velocidad del LEM relativa al módulo de comando al dejarse a la deriva. El punto A es el apogeo de la trayectoria elíptica de choque y la masa de la Luna es 0.0123 veces la masa de la Tierra. Problema de Gravitación.
Determinar la velocidad de escape en la superficie de Mercurio cuya masa es M=3.31·1023 kg y su radio R=2.44·106 m Cuestion de Gravitación.
Un satélite terrestre está en una órbita circular de radio r=7.19 Mm. a) ¿Cuál es el módulo de la velocidad del satélite? b) ¿Cuál es el período de su órbita? Cuestion de Gravitación.
