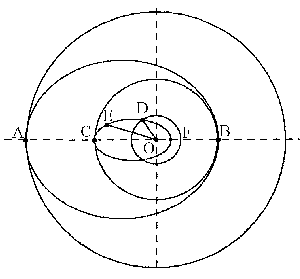
Un vehículo se encuentra en una órbita circular a 600 km de altura sobre la superficie terrestre, moviéndose en sentido horario. Se pretende transferir dicho vehículo a otra órbita circular a 300 km de altura sobre la superficie terrestre. Para ello, el vehículo describirá una órbita elíptica de transición desde A hasta B. a) Calcular la velocidad del vehículo en la primera órbita circular. b) Calcular el incremento de velocidad que hay que proporcionar al vehículo en el punto A para transferirlo a la órbita elíptica de transición. c) Para producir el cambio de velocidad los motores del vehículo ejercen una fuerza de frenado de 1675.8 N. Si la masa del vehículo es de 600 kg, ¿durante cuánto tiempo debe ejercerse esta fuerza? d) Calcular el período de la órbita de transición. e) Calcular el incremento de velocidad que hay que proporcionar al vehículo en el punto B para transferirlo a la segunda órbita circular. f) Una vez en la segunda órbita circular, al pasar por el punto C, al vehículo se le disminuye la velocidad en 575.6 m/s, situándolo en una nueva órbita elíptica de retorno a la Tierra, órbita cuyo apogeo es el punto C. Calcular el ángulo FOD que define el punto de aterrizaje (punto D) y la altura a la cual estará el vehículo en el punto E,cuando el ángulo FOE sea 160o.