Gravitación

Se pretende transportar material de reparación desde la Tierra a una estación espacial que está describiendo una órbita circular a 600 km sobre la superficie de la Tierra. Para ello se utiliza una lanzadera que describirá la órbita elíptica de aproximación que aparece en la figura (de la que se dibuja el tramo BA). La lanzadera asciende 60 km desde la superficie de la Tierra, apaga los motores en el punto B y con la velocidad v_B (de la que se sabe forma 60^o con su radio vector como indica el dibujo) entra en la órbita elíptica, realizándose el acoplamiento de la lanzadera y la estación espacial en el punto A, donde ambas órbitas son tangentes. Determinar: a) la velocidad y el periodo en la órbita de la estación espacial; b) la velocidad v_B de la lanzadera; c) el incremento de velocidad de la lanzadera en el punto A para que tenga lugar el acoplamiento; d) el ángulo β que define la posición de la estación espacial en el instante en que la lanzadera está en B, sabiendo que la lanzadera tarda 20 minutos en llegar al punto de encuentro A; e) después de cumplir su misión, la lanzadera vuelve a la tierra. Calcular la disminución de velocidad de la lanzadera en el punto D (apogeo de la órbita elíptica de regreso, señalada en la figura, tramo DC) para que aterrice siguiendo esa órbita en el punto C.
Datos: R_Tierra=6370 km; M_Tierra=6·10²⁴ kg; G=6.67·10^-11 Nm²/kg².

Problema de Gravitación. Aparece en la convocatoria de FEB2004.

Suponer que se realiza un aterrizaje en un planeta de otro sistema solar que tiene la misma masa por unidad de volumen que la Tierra, pero su radio es 10 veces el de la Tierra. ¿Cuál sería tu peso en ese planeta comparado con el que tienes en la Tierra?

Problema de Gravitación.

El programa de un vuelo no tripulado para explorar el planeta Marte establece que el vehículo de regreso a la Tierra describirá en primer lugar una órbita circular alrededor del planeta. Al pasar por el punto A será transferido a una órbita elíptica de transición encendiendo sus motores para aumentar su velocidad en Δv_A. Cuando pase por el punto B, el vehículo volverá a ser transferido a una segunda órbita de transición, disminuyendo la velocidad en Δv_B. Finalmente, al pasar el vehículo por el punto C se aumentará su velocidad en Δv_C para situarlo en la trayectoria parabólica de retorno. Sabiendo que el radio del planeta Marte es R=3400 km, que su masa es 0.108 veces la masa de la Tierra y que las alturas de los puntos A, B y C son d_A=2500 km, d_B=90000 km y d_C=1000 km respectivamente, determinar: a) el aumento de velocidad Δv_A que es necesario proporcionar al vehículo en el punto A para transferirlo a la primera órbita de transición; b) la variación de velocidad Δv_B que es necesario proporcionar al vehículo en el punto B para transferirlo a la segunda órbita de transición; c) el aumento mínimo de velocidad Δv_C que es preciso proporcionar al vehículo en el punto C para situarlo en una trayectoria de escape; d) el tiempo empleado por el vehículo para recorrer la primera órbita de transición entre los puntos A y B.

Problema de Gravitación.

Con el fin de reparar los paneles solares de un satélite terrestre, de comunicaciones, situado en una órbita geosíncrona (es decir permanece fijo respecto al suelo terrestre) se envía a unos técnicos en un vehículo espacial. Sabiendo que dicho vehículo describe inicialmente una órbita circular, coplanaria y en el mismo sentido que el satélite a 650 km sobre la superficie de la tierra, antes de pasar a la órbita elíptica de transición que le lleve hasta el satélite (ver figura). Determinar. a) El radio R de la órbita que describe el satélite así como su velocidad. b) El incremento de velocidad que deben de proporcionar los motores al vehículo en el punto A para transferirlo a la órbita elíptica de transición, así como el incremento de velocidad en B para acoplarse al satélite. c) El ángulo θ que define la posición del satélite, respecto al punto de encuentro, en el momento que el vehículo pasa a la trayectoria de transición .Masa de la tierra 6·10²⁴ kg ; radio de la tierra 6370 km; constante de Gravitación universal G= 6.67·10^-11 N·m²/kg².

Problema de Gravitación.

Se pretende colocar una sonda espacial en una órbita circular de 4000 km de radio alrededor de Marte. Para ello cuando la sonda llega a A, punto de su trayectoria de aproximación más cercano a Marte, se inserta primero en una órbita elíptica de transferencia reduciendo su velocidad en Δv_A. Esta órbita la lleva hasta el punto B con una velocidad muy reducida. Ahí la sonda es insertada en una segunda órbita de transferencia reduciendo su velocidad en Δv_B. Finalmente cuando llega al punto C se introduce en la órbita circular deseada reduciendo su velocidad en Δv_C. Sabiendo que r_A=9000 km, que Δv_A= 440 m/s y que la sonda se aproxima a A siguiendo una trayectoria parabólica, hallar: a) la distancia r_B del centro de Marte al punto B; b) el incremento de velocidad Δv_B; c) el tiempo que tarda la sonda en pasar de A hasta B en su primera órbita de transferencia; d) el incremento de velocidad Δv_C; e) la ecuación de la segunda órbita de transferencia.
G=6.67•10^-11Nm²/kg² y M_Marte=6.444•10²³kg.

Problema de Gravitación. Aparece en la convocatoria de FEB2007.

Un cometa se mueve según una órbita elíptica alrededor del Sol. En qué punto de su órbita tiene mayor valor: a) la velocidad del cometa; b) la energía potencial del sistema cometa-Sol; c) la energía cinética del cometa; d) la energía total del sistema cometa-Sol.

Cuestion de Gravitación.

Un satélite gira a una distancia muy próxima a la Luna describiendo una órbita circular. La gravedad lunar es 1/6 de la terrestre y el radio 1/4 del terrestre. Si el satélite girara alrededor de la Tierra, también muy próximo a ella, con un período T_T, ¿cuál sería el período de revolución del satélite lunar?

Problema de Gravitación.

Dos estaciones espaciales S₁ y S₂ recorren en sentido antihorario órbitas coplanarias en torno a la Tierra de radios r₀=7000 km y 8r₀ respectivamente. 1º) Se desea enviar un vehículo desde S₁ hasta S₂, y para ello ha de ser lanzado tangencialmente a la órbita de S₁ y ha de alcanzar a S₂ con una velocidad tangente a la órbita de ésta. Tras un período muy corto de vuelo propulsado, el vehículo irá en vuelo libre de S₁ a S₂. a) Determinar la velocidad de lanzamiento del vehículo (velocidad relativa a S₁). b) Determinar el ángulo θ que define la posición a ocupar por S₂ en el momento del lanzamiento. 2º) Inmediatamente después de que S₁ lance el vehículo, se pretende hacer regresar a la Tierra dicha estación espacial disminuyendo su velocidad de forma prácticamente instantánea. De esta forma se inicia una trayectoria elíptica de acercamiento a la Tierra, trayectoria cuyo apogeo es el mismo punto en que S₁ lanzó el vehículo. Determinar la velocidad de aterrizaje, si el ángulo que define el punto en que aquél se produce es -45^o.

Problema de Gravitación.

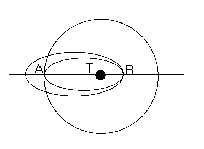
Un vehículo espacial, de masa m=1000 toneladas, describe una órbita circular en torno a la Tierra, completando una vuelta cada 10 horas. Cuando está en la posición A se le comunica un incremento de velocidad Dv=-1300 m/s, pasando de esta forma a describir una órbita elíptica. Determinar:
a) El semieje mayor de dicha órbita.
b) La velocidad en el punto B.
A continuación, en el punto B, se produce un incremento de energía en el vehículo DE=+1,29·10¹² J, con lo que el vehículo pasa a describir una segunda órbita elíptica. Determinar:
c) El periodo T de esta segunda órbita elíptica.
Datos: G = 6,67·10^-11 N·m²/kg², M_Tierra = 6·10²⁴ kg, R_Tierra = 6370 km.

Problema de Gravitación. Aparece en la convocatoria de SEP1998.

Un satélite recorre una órbita circular situada 10000 km por encima de la superficie terrestre. En el punto A se reduce su velocidad para situar al satélite en una órbita elíptica de transición cuya altitud mínima es de 5000 km en el punto B. En el punto B se vuelve a reducir la velocidad del satélite para introducirlo en una trayectoria circular. Por último, tras dar una vuelta completa y pasar de nuevo por el punto B se reduce la velocidad nuevamente para insertar el vehículo en una trayectoria elíptica de aterrizaje cuyo apogeo es el punto B. Determinar: a) la disminución de velocidad Δv_A que hay que proporcionar al vehículo en el punto A para pasar de la órbita circular grande a la elíptica de transición; b) el período de la trayectoria elíptica de transición; c) la excentricidad de dicha órbita; d) la disminución de velocidad Δv_B que se debe comunicar al satélite en el punto B para situarlo en la trayectoria circular pequeña; e) si la reducción de velocidad del satélite para la inserción en la trayectoria de aterrizaje es de 2100 m/s, ¿a qué ángulo se producirá éste?
Datos: masa de la Tierra: M=6•10²⁴ kg; radio de la Tierra: R=6370 km; constante de gravitación universal: G=6.67•10^-11 Nm²/kg².

Problema de Gravitación. Aparece en la convocatoria de FEB2008.