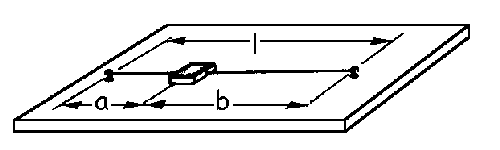
Problema de Movimiento Oscilatorio. Aparece en la convocatoria de JUL2007.
Problema de Movimiento Oscilatorio.
Problema de Movimiento Oscilatorio.
Problema de Movimiento Oscilatorio. Aparece en la convocatoria de FEB2018.
Tipos de amortiguamiento. Describa sus características fundamentales.
Cuestion de Movimiento Oscilatorio.
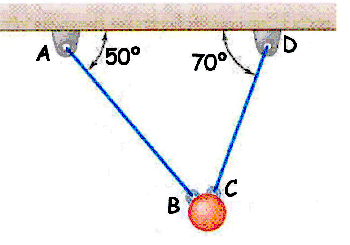
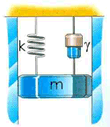

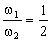 , teniendo en cuenta que las amplitudes guardan una relación inversa a la anterior y que la diferencia de fase es de 45o.
, teniendo en cuenta que las amplitudes guardan una relación inversa a la anterior y que la diferencia de fase es de 45o.
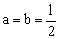 .
.