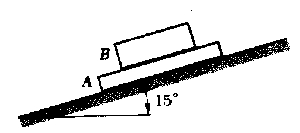
Problema de Trabajo y Energía.
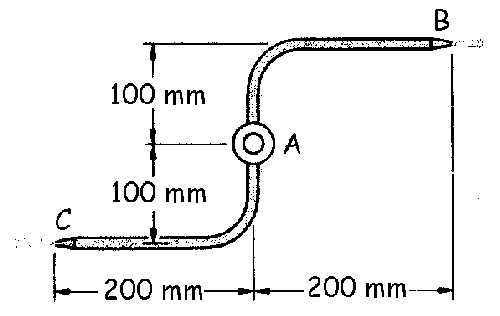
Problema de Dinámica de los Sistemas de Partículas.
Problema de Dinámica de los Sistemas de Partículas.
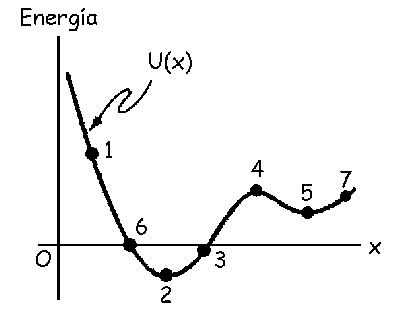
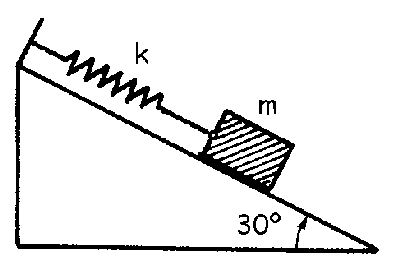
Problema de Movimiento Oscilatorio.
Demostrar que si F está en Newton y m en kg/m las unidades de la velocidad, son m/s: 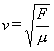
Problema de Introducción (Magnitudes y Vectores).
Problema de Movimiento Ondulatorio.
Problema de Propiedades Elásticas de los Sólidos.
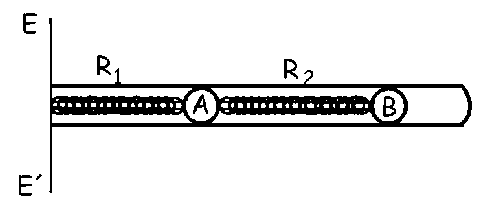
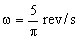 . Las bolitas A y B de igual masa m=60 g resbalan sin rozamiento a lo largo del tubo. Si las longitudes de los resortes R1 y R2, sin deformar, son 50 cm y 60 cm, y sus constantes elásticas 150 N/m y 160 N/m respectivamente, calcule el aumento de longitud de cada resorte y las tensiones en cada uno de ellos.
. Las bolitas A y B de igual masa m=60 g resbalan sin rozamiento a lo largo del tubo. Si las longitudes de los resortes R1 y R2, sin deformar, son 50 cm y 60 cm, y sus constantes elásticas 150 N/m y 160 N/m respectivamente, calcule el aumento de longitud de cada resorte y las tensiones en cada uno de ellos.