Física I

Tres esferas idénticas, A, B y C están en línea recta sobre un plano horizontal. Se lanza A contra B con una velocidad de 4 m/s. Determinar las velocidades de las tres esferas después de chocar A con B, B con C y A con B por segunda vez. El coeficiente de restitución es e=0.5.

Problema de Dinámica de los Sistemas de Partículas.

La boquilla mostrada en la figura descarga un caudal de agua de 0.95 m³/min con una velocidad v_A de 40 m/s. La corriente es desviada por el álabe fijo AB. Hallar el sistema fuerza-par que ha de aplicarse en C para que el álabe no se mueva.

Problema de Dinámica de los Sistemas de Partículas.

El conjunto del peso de 5 kg, el resorte y la base B solidarios caen verticalmente una distancia h=10 cm, partiendo del reposo, sin que se alargue el resorte. Cuando la base B choca contra el soporte fijo, un tope la sujeta y se observa que el peso cae una distancia adicional de 5 cm mientras se alarga el resorte. Hallar la frecuencia ν de la vibración subsiguiente.

Problema de Movimiento Oscilatorio.

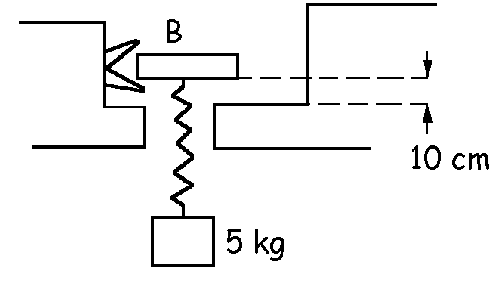
Determinar la frecuencia de oscilación del objeto de masa m en los dos casos de la figura.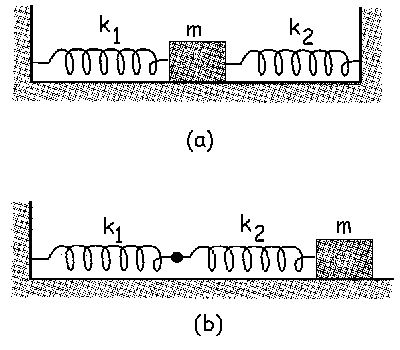

Problema de Movimiento Oscilatorio.

Determinar el momento del vector F=2i–j+3k, aplicado en el punto P=(2,5,3): a) con respecto al origen de coordenadas; b) con respecto al punto O´=(1,2,-1).

Problema de Introducción (Magnitudes y Vectores).

La ecuación de un movimiento ondulatorio es y=2cos2λ(5t-0.1x), estando x en m y t en s. x es la distancia al punto donde se inicia la perturbación o foco y t es el tiempo transcurrido. Se pide: a) la longitud de onda; b) el período del movimiento ondulatorio; c) su frecuencia; d) velocidad de propagación; e) velocidad máxima de vibración de las partículas del medio.

Problema de Movimiento Ondulatorio.

Una onda sonora cuya intensidad es 10^-2 W/m ² al penetrar en un medio absorbente de 1 m de espesor, tiene al salir del mismo una amplitud que es la cuarta parte de la que tenía al incidir en el medio absorbente. Determinar la intensidad de la onda a la salida, el coeficiente de absorción del material y su espesor de semiabsorción.

Problema de Movimiento Ondulatorio.

Un hombre trabaja en su finca situada a 300 m del cruce con una carretera. En el momento de pasar por el cruce un coche a 72 km/h percibe un motor de 600 explosiones por minuto con una cierta sensación sonora. Si al cabo de 20 s deja de percibirlo, ¿cuál es la distancia que le separa del vehículo, la frecuencia percibida en ese instante y la sensación sonora que le produce cuando estaba en el cruce?

Problema de Movimiento Ondulatorio.

Un ascensor de 2500 kg está sostenido por cuatro cables de acero trenzado, cada uno de los cuales tiene una sección recta eficaz de 1.2 cm². Calcular la máxima aceleración hacia arriba que puede darse al ascensor si el esfuerzo en cada cable no puede exceder el 35% del correspondiente al límite elástico. Límite elástico del acero: 25·10⁷ N/m²

Problema de Propiedades Elásticas de los Sólidos.

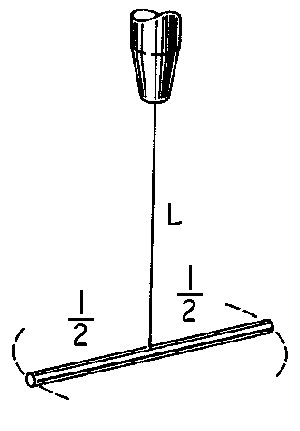
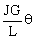Una varilla uniforme de longitud l y masa m está suspendida por su punto medio de un alambre de longitud L. El momento resistente del alambre es proporcional al ángulo de torsión q e igual a , donde J es el momento polar de la sección recta del alambre y G es el módulo de cizalladura. Encontrar la expresión del período T de oscilación de la barra cuando realiza un movimiento de rotación en torno al eje del alambre.

Problema de Propiedades Elásticas de los Sólidos.