Física I

La barra uniforme de la figura pesa 100 N y puede girar sin rozamientos en torno al pasador situado en B. La constante y longitud natural del resorte son k=800 N/m y l0=15 cm respectivamente. Si la barra lleva una velocidad angular de 3 rad/s en sentido horario cuando está horizontal determinar: a) la aceleración angular de la barra así como las reacciones (Fx y Fy) en el pasador en la posición de la figura; b) la velocidad angular de la barra cuando ésta está vertical, estando A directamente encima de B.
Momento de inercia de una barra respecto de su punto medio

Problema de Dinámica del Sólido Rígido. Aparece en la convocatoria de ENE2020.

Dos naves espaciales, Galileo (G) y Sócrates (S), se encuentran en dos órbitas circulares en torno a la Tierra, moviéndose con velocidades de 7072.84 m/s y 7561.18 m/s, ambas en sentido horario. Se quiere hacer que la nave Galileo se acople con Sócrates justo en el punto P. Para ello, Galileo parte del punto G y Sócrates del punto S en un cierto instante. Al llegar al punto A, Galileo disminuirá su velocidad para situarse en una órbita elíptica de transición (elipse AP), y posteriormente volverá a disminuirla en el punto P acoplándose con Sócrates. Determinar: a) incremento de velocidad que debe producirse en la nave Galileo en el punto A para pasar de la primera órbita circular a la órbita elíptica de transición; b) incremento de velocidad que debe producirse en dicho vehículo en el punto P para transferirlo a la segunda órbita circular; c) velocidad areolar del vehículo Galileo en la primera órbita circular; d) período de la órbita de transición; e) el ángulo q que define la posición a ocupar por el vehículo Sócrates al inicio de la maniobra para que el acoplamiento se produzca en el punto indicado (despreciar el tiempo invertido en los incrementos de velocidad).
Datos: masa de la Tierra M=6·1024 kg; radio de la Tierra R=6370 km; constante de gravitación universal G=6.67·10-11 Nm2/kg2.

Problema de Gravitación. Aparece en la convocatoria de JUL2001.

Un observador dentro de un globo en reposo sobre tierra está situado en el punto medio de la línea que une dos tubos sonoros separados entre si una distancia de 200 m. Uno de ellos es un tubo abierto de 2.55 m de longitud que vibra en su segundo armónico; el otro tiene una frecuencia 10 Hz más que el anterior. a) ¿Cuáles son las frecuencias de los tubos? b) Ambos focos sonoros, que pueden desplazarse a lo largo de la línea recta que los une, empiezan a emitir en el mismo instante. Si el primer foco se mueve hacia el observador con una velocidad de 30 m/s, determinar la velocidad que debe llevar el segundo foco para que el observador reciba dos señales con la misma frecuencia y el valor de la misma; c) si los focos se mueven en sentidos opuestos con la misma velocidad (30 m/s), y el observador en globo empieza su ascenso a 20 m/s en dirección perpendicular a la recta que une los tubos, ¿qué pulsación percibirá cuando se encuentre a 50 m de altura sabiendo que sopla viento en sentido del primer foco al segundo con una velocidad de 5 m/s? Velocidad de propagación del sonido en aire en calma: 340 m/s.

Problema de Movimiento Ondulatorio. Aparece en la convocatoria de SEP2004.

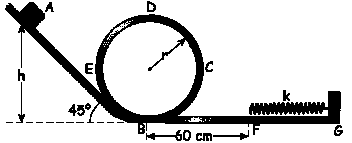
Un bloque de 600 g se suelta en la posición A, desliza a lo largo del plano inclinado 45º hasta B, a continuación describe el bucle BCDEB, desliza a lo largo del plano horizontal BF y finalmente comprime un muelle de constante k=500 N/m cuyo extremo libre dista 60 cm de B. a) Calcular la máxima deformación del muelle, sabiendo que h=2.5 m, el radio del bucle r=0.5 m, y el coeficiente dinámico de rozamiento en el plano horizontal BG e inclinado AB es de 0.3. Se supone que no hay rozamiento en el bucle. b) Hallar la reacción en la posición D; c) a continuación se cuelga ese mismo muelle verticalmente de uno de sus extremos llevando en el otro un peso de 1000 N. A partir de la posición de equilibrio se estira el muelle 10 cm y se le deja en libertad en un medio que ofrece una resistencia de 2.5v en N, siendo v la velocidad del peso suspendido en el muelle. ¿De qué tipo de amortiguamiento se trata? d) Escribe la ecuación del movimiento de la masa, suponiendo que el desfase inicial es nulo; e) si además sometemos al resorte a una fuerza exterior de 25·104cosωt dinas, calcula la amplitud de las oscilaciones en función de ω y la amplitud máxima.

Problema de Movimiento Oscilatorio. Aparece en la convocatoria de SEP2004.