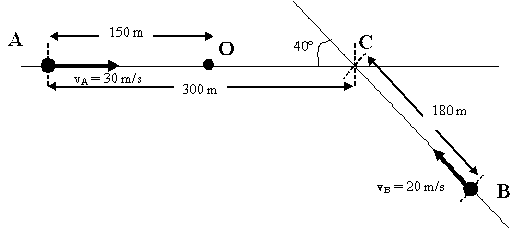
Considérese la situación de la figura, en la que dos coches A y B circulan por sendas carreteras, como se indica. Un observador O se encuentra en la posición indicada, moviéndose sobre la recta AC a una determinada velocidad v. La temperatura ambiente es de 26 oC y sopla viento (con velocidad de 8 m/s) en la dirección y sentido de avance del coche A. Determinar:
a) la velocidad del observador si la frecuencia percibida por éste de las ondas procedentes del coche A, al hacer sonar su bocina (νA = 200 Hz) es 225 Hz.
b) para la situación al cabo de 5 s respecto a la situación inicial dibujada, la frecuencia percibida por un observador en el coche B de las ondas emitidas por la bocina del coche A.
c) Considérese ahora que la bocina del coche B emite una onda sincrónica con la del coche A (νB = 200 Hz). Para la situación inicialmente dibujada, determinar el valor del desfase (δ) en un punto sobre la recta AB a 200 m de A. ¿Se tiene situación de máximo o mínimo?
(Velocidad del sonido a 0 oC y con el viento en calma vS=335 m/s)