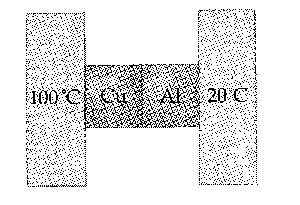
¿A qué temperatura se tiene el mismo valor en las escalas Farenheit y Celsius?
Problema de Calor y Primer Principio de la Termodinámica.
Problema de Calor y Primer Principio de la Termodinámica.
Problema de Teoría Cinética de los Gases.
Problema de Teoría Cinética de los Gases.
Problema de Entropia y Segundo Principio de la Termodinámica.
En la difracción de rayos X por los cristales, ¿cuál es la condición de Bragg?
Cuestion de Difracción.